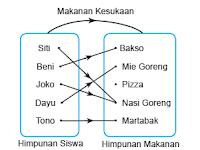
"Misalkan A dan B adalah himpunan. Relasi dari himpunan A dan B dihubungkan dengan aturan pengaitan/pemasangan anggota-anggota A dengan anggota-anggota B".
Terdapat sifat-sifat dari relasi sebagai berikut.
1. Sifat Reflektif
Misalkan R sebuah relasi yang didefinisikan pada himpunan P. Relasi R dikatakan bersifat refleksif jika untuk setiap p є P berlaku (p,p) є R.
Contoh : Diberikan himpunan P = {1,2,3}. Didefinisikan relasi R pada himpunan P dengan hasil relasi adalah himpunan S={(1,1,), (1,2), (2,3), (3,3), (3,2)}. Relasi R tersebut bersifat reflektif sebab setiap anggota himpunan P berpasangan atau berelasi dengan dirinya sendiri.
2. Sifat Simetris
Misalkan R sebuah relasi pada himpunan P. Relasi R dikatakan bersifat simetris apabila untuk setiap (x,y) є R berlaku (y, x) є R.
Contoh : Diberikan himpunan P = {1,,2,3}. Didefinisikan relasi R pada himpunan P dengan R = {(1,1,), (1,2), (1,3), (2,2), (2,1), (3,1), (3,3)}. Relasi R bersifat simetris sebab untuk setiap (x,y) є R berlaku (y,x) є R.
3. Sifat Transitif
Misalkan R sebuah relasi pada himpunan P. Relasi R bersifat transitif apabila untuk setiap (x,y) є R dan (y,z) є R maka berlaku (x,z) є R.
Contoh : Diberikan himpunan P={1,2,3} didefinisikan relasi pada himpunan P dengan hasil relasi adalah himpunan R={(1,1), (1,2), (2,2), (2,1), (3,3)}. Relasi R tersebut bersifat transitif sebab (x,y) є R dan (y,z) є R maka berlaku (x,z) є R.
4. Sifat Antisimetris
Misalkan R sebuah relasi pada sebuah himpunan P. Relasi R dikatakan bersifat antisimetri apabila untuk setiap x,y) є R dan (y, x) є R maka berlaku (y = x) є R.
Contoh : Diberikan himpunan C = {2, 4, 5}. Didefinisikan R pada himpunan C dengan R = {(a,b) є a kelipatan b} sehingga diperoleh R= {(2,2), (4,4), (5,5) (4,2)} Relasi R tersebut bersifat antisimetris.
Relasi juga memiliki pendefinisian sebagai berikut :
" Misalkan R sebuah relasi pada himpunan P. Relasi R dikatakan relasi ekuivalensi jika dan hanya jika relasi R memnuhi sifat reflektif, simetris, dan transitif".
B. Sifat - Sifat Fungsi
Fungsi dapat dinyatakan dengan definisi sebagai berikut:
"Misalkan A dan B adalah himpunan. Fungsi f dari A ke B adalah suatu aturan pengaitan yang memasangkan setiap anggota himpunan A dengan tepat satu anggota himpunan B.
Dapat disimbolkan dengan
f : A --> B, dibaca fungsi f meemtakan setiap anggota himpunan A dengan tepat satu anggota himpunan B.
Untuk memahami sifat fungsi dapat mempelajari berdasarkan jenis-jenis fungsi seperti fungsi naik dan turun, fungsi ganjil dan genap. Hal ini akan dibahas pada pertemuan berikutnya.