Rangkuman Materi Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap Lengkap
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap Lengkap
Rangkuman Materi Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap Lengkap
Pengertian Matriks - Dalam artikel kali ini akan membahas materi mengenai definisi atau pengertian matriks matematika serta unsur - unsur yang ada di dalamnya. Untuk lebih jelasnya perhatikan baik - baik pembahasan berikut ini:
Dalam matematika, matriks merupakan kumpulan bilangan, simbol atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan - bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks.
Selanjutnya, secara umum matriks bisa diartikan sebagai sebuah susunan atau kumpulan dari beberapa bilangan yang disusun berdasarkan kepada baris dan kolom yang bentuknya persegi panjang. Matriks mempunyai ciri khas khusus dimana biasanya bilangan yang menjadi elemen dari sebuah matriks disusun dengan diapit oleh tanda kurung siku [] namun terkadang ada juga elemen matriks yang diapit oleh tanda kurung biasa ().
Ukuran dari sebuah matriks disebut dengan ordo yang menjelasakan jumlah dari kolom dan baris yang ada di dalam matriks tersebut.
Ukuran dari sebuah matriks bisa disimbolkan dengan rumus sebagai berikut :
Amxn
A = Nama Matriks
m = jumlah baris
n = jumlah kolom
mxn = ordo matriks
Contoh :

Jangan sampai terbalik dalam membaca ordo matriks, ingatlah bahwa ordo matriks merupakan banyaknya baris dikali dengan banyaknya kolom.
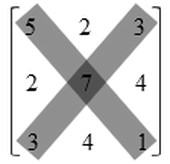
Di dalam materi mengenai matriks juga dikenal dengan istilah diagonal. Terdapat dua jenis diagonal di dalam matriks yaitu diagonal utama dan diagonal sekunder. Diagonal utama merupakan garis miring yang ditarik dari sisi kiri atas matriks menuju sisi kanan bawah matriks. Sementara diagonal sekunder adalah kebalikannya. Seperti bisa dilihat pada gambar di bawah ini :

Matriks Persegi
Merupakan matriks yang memiliki baris dan kolom yang sama, misalnya 4x4, 2x2, atau 5x5. Sehingga ordonya dialmbangkan n x n.
Matriks Baris
Adalah matriks yang hanya memiliki satu buah baris namun memiliki beberapa kolom. Matriks ini ordonya adalah 1 x n dimana n harus lebih besar dari 1. Contohnya 1 x 2, 1 x 4, 1 x 5, 1 x 6, dan lain sebagainya.
Matriks Kolom
Merupakan kebalikan dari matriks baris. Hanya terdiri dari satu kolom namun memiliki beberapa baris. Ordo dari matriks ini adalah n x 1 dimana n harus lebih besar dari 1. Contohnya adalah 2 x 1, 3 x 1, 4 x 1, 5 x 1, dan lain sebagainya.\

Matriks Mendatar
Adalah matriks yang mempunyai jumlah kolom yang lebih banyak dibandingkan jumlah barisnya. Contohnya adalah 3 x 5, 4 x 6, dan lain sebagainya.
Matriks Tegak
Merupakan kebalikan dari matriks mendatar dimana jumlah barisnya lebih banyak dibandingkan jumlah kolomnya. Contohnya adalah 6 x 3, 4 x 2, 8 x 5, dan lain sebagainya.

Matriks Nol
Merupakan matriks dengan ordo m x n dimana seluruh elemennya memiliki nilai nol.
Matriks Diagonal
Merupakan matriks persegi yang elemennya bernilai nol kecuali pada diagonal utamanya.
Matriks Identitas
Adalah matriks yang diagonal utamanya di isi dengan elemen bernilai 1 sementara elemen yang lain nilainya adalah nol.

Matriks Segitiga Atas
Adalah matriks yang keseluruhan nilai di bawah diagonal utamanya adalah nol.
Matriks Segitiga Bawah
Merupakan kebalikan dari matriks segitiga atas dimana seluruh elemen yang ada di atas diagonal utamanya bernilai nol.
Matriks Simetris
Merupakan sebuah matriks dimana elemen yang ada di atas dan di bawah diagonal utamanya memiliki susunan nilai yang sama.
Matriks Skalar
Merupakan matriks yang memiliki elemen diagonal utama bernilai sama sementara elemen yang lain nilainya adalah nol.

Demikianlah pembahasan materi mengenai Pengertian dan Jenis-jenis Matriks Matematika Lengkap. Semoga artikel ini bisa memberikan pengetahuan yang baik bagi kalian terutama tentang matriks matematika. Selamat belajar!

Definisi Matriks dan Jenis - Jenis Matriks Matematika
Dalam matematika, matriks merupakan kumpulan bilangan, simbol atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan - bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks.
Selanjutnya, secara umum matriks bisa diartikan sebagai sebuah susunan atau kumpulan dari beberapa bilangan yang disusun berdasarkan kepada baris dan kolom yang bentuknya persegi panjang. Matriks mempunyai ciri khas khusus dimana biasanya bilangan yang menjadi elemen dari sebuah matriks disusun dengan diapit oleh tanda kurung siku [] namun terkadang ada juga elemen matriks yang diapit oleh tanda kurung biasa ().
Ukuran dari sebuah matriks disebut dengan ordo yang menjelasakan jumlah dari kolom dan baris yang ada di dalam matriks tersebut.
Ukuran dari sebuah matriks bisa disimbolkan dengan rumus sebagai berikut :
Amxn
A = Nama Matriks
m = jumlah baris
n = jumlah kolom
mxn = ordo matriks
Contoh :

Jangan sampai terbalik dalam membaca ordo matriks, ingatlah bahwa ordo matriks merupakan banyaknya baris dikali dengan banyaknya kolom.
Diagonal Utama dan Diagonal Sekunder Pada Matriks
Di dalam materi mengenai matriks juga dikenal dengan istilah diagonal. Terdapat dua jenis diagonal di dalam matriks yaitu diagonal utama dan diagonal sekunder. Diagonal utama merupakan garis miring yang ditarik dari sisi kiri atas matriks menuju sisi kanan bawah matriks. Sementara diagonal sekunder adalah kebalikannya. Seperti bisa dilihat pada gambar di bawah ini :

Jenis - Jenis Matriks Berdasarkan Banyaknya Baris dan Kolom
Matriks Persegi
Merupakan matriks yang memiliki baris dan kolom yang sama, misalnya 4x4, 2x2, atau 5x5. Sehingga ordonya dialmbangkan n x n.
Matriks Baris
Adalah matriks yang hanya memiliki satu buah baris namun memiliki beberapa kolom. Matriks ini ordonya adalah 1 x n dimana n harus lebih besar dari 1. Contohnya 1 x 2, 1 x 4, 1 x 5, 1 x 6, dan lain sebagainya.
Matriks Kolom
Merupakan kebalikan dari matriks baris. Hanya terdiri dari satu kolom namun memiliki beberapa baris. Ordo dari matriks ini adalah n x 1 dimana n harus lebih besar dari 1. Contohnya adalah 2 x 1, 3 x 1, 4 x 1, 5 x 1, dan lain sebagainya.\

Matriks Mendatar
Adalah matriks yang mempunyai jumlah kolom yang lebih banyak dibandingkan jumlah barisnya. Contohnya adalah 3 x 5, 4 x 6, dan lain sebagainya.
Matriks Tegak
Merupakan kebalikan dari matriks mendatar dimana jumlah barisnya lebih banyak dibandingkan jumlah kolomnya. Contohnya adalah 6 x 3, 4 x 2, 8 x 5, dan lain sebagainya.

Jenis Matriks Berdasarkan Pada Pola Elemennya
Matriks Nol
Merupakan matriks dengan ordo m x n dimana seluruh elemennya memiliki nilai nol.
Matriks Diagonal
Merupakan matriks persegi yang elemennya bernilai nol kecuali pada diagonal utamanya.
Matriks Identitas
Adalah matriks yang diagonal utamanya di isi dengan elemen bernilai 1 sementara elemen yang lain nilainya adalah nol.

Matriks Segitiga Atas
Adalah matriks yang keseluruhan nilai di bawah diagonal utamanya adalah nol.
Matriks Segitiga Bawah
Merupakan kebalikan dari matriks segitiga atas dimana seluruh elemen yang ada di atas diagonal utamanya bernilai nol.
Matriks Simetris
Merupakan sebuah matriks dimana elemen yang ada di atas dan di bawah diagonal utamanya memiliki susunan nilai yang sama.
Matriks Skalar
Merupakan matriks yang memiliki elemen diagonal utama bernilai sama sementara elemen yang lain nilainya adalah nol.

Demikianlah pembahasan materi mengenai Pengertian dan Jenis-jenis Matriks Matematika Lengkap. Semoga artikel ini bisa memberikan pengetahuan yang baik bagi kalian terutama tentang matriks matematika. Selamat belajar!
