Rangkuman Materi Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Rangkuman Materi Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Pengertian Sifat Komutatif Matematika - Selain Sifat Distributif yang telah dijelaskan pada artikel sebelumnya, di dalam matematika juga ada yang dinamakan dengan sifat komutatif. Sifat komutatif diartikan sebagai sia pertukaran di dalam sebuah operasi hitung matematika. Perhatikan baik - baik perhitungan gambar berikut ini :
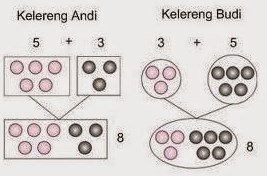
Berdasarkan gambar di atas kita bisa menyimpulkan bawa sifat komutatif di dalam matematika memenuhi rumus a + b = b + a dimana a dan b merupakan bilangan bulat. Sifat ini tidak hanya berlaku pada operasi penjumlahan namun juga berlaku pada operasi perkalian (a x b = b x a). Jadi, pada sifat komutatif matematika diperbolehkan melakukan pertukaran angka di dalam penjumlahan dan perkalian dengan hasil yang tetap sama.
A. Sifat Komutatif Pada Operai Hitun Penjumlahan
Contoh :
Hitunglah hasil dari 10.483 + 32.514 = ....
Penyelesaian :
Hasil dari 10.483 + 32.514 = 42.997
Jika kedua bilangan tersebut kita tukar tempatnya, maka hasilnya akan tetap sama :
32.514 + 10.483 = 42.997

Berdasarkan gambar di atas kita bisa menyimpulkan bawa sifat komutatif di dalam matematika memenuhi rumus a + b = b + a dimana a dan b merupakan bilangan bulat. Sifat ini tidak hanya berlaku pada operasi penjumlahan namun juga berlaku pada operasi perkalian (a x b = b x a). Jadi, pada sifat komutatif matematika diperbolehkan melakukan pertukaran angka di dalam penjumlahan dan perkalian dengan hasil yang tetap sama.
Pembahasan Contoh Soal Sifat Komutatif Matematika
A. Sifat Komutatif Pada Operai Hitun Penjumlahan
Contoh :
Hitunglah hasil dari 10.483 + 32.514 = ....
Penyelesaian :
Hasil dari 10.483 + 32.514 = 42.997
Jika kedua bilangan tersebut kita tukar tempatnya, maka hasilnya akan tetap sama :
32.514 + 10.483 = 42.997
Artinya, hukum komutatif berlaku untuk operasi hitung penjumlahan.
B. Sifat Komutatif Pada Operasi Hitung Pengurangan
Contoh :
52.841 - 30.512 = ....
Penyelesaian :
52.841 - 30.512 = 22.329
Seandainya posisi kedua bilangan tersebut kita tukar maka hasilnya akan berbeda :
30.512 - 52.841 = -22.329
Terlihat bahwa hasilnya menjadi negatif. Artinya, sifat komutatif tidak berlaku untuk operasi hitung pengurangan (a - b ≠ b - a)
C. Sifat Komutatif Pada Operasi Hitung Perkalian
Contoh :
12 x 24 = ....
Penyelesaian :
12 x 24 = 288
Untuk membuktikan apakah sifat komutatif berlaku pada operasi hitung perkalian maka kita tukar posisi kedua bilangan tersebut :
24 x 12 = 288
Ternyata hasilnya tetap sama. Artinya, sifat komutatif berlaku pada operasi hitung perkalian.
D. Sifat Komutatif Pada Operasi Hitung Pembagian
Contoh :
40 : 10 = 4
Jika kedua bilangan tersebut kita tukar apakah hasilnya akan tetap sama ?
10 : 40 = 0,25
Ternyata setelah posisinya kita tukar hasil yang didapatkan berbeda. Maka disimplkan bahwa sifat komutatif tidak bisa berlaku di dalam operasi hitung pembagian (a : b ≠ b : a)
Cukup sampai disini dulu pembahasan materi mengenai Pengertian Sifat Komutatif Matematika Dilengkapi Pembahasan Contoh Soal. Semoga kalian bisa memahami penjelasan materi dan contoh soal yang telah disampaikan di atas dengan baik sehingga kalian tidak akan mengalami kesulitan dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar!