Rangkuman Materi Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus Lengkap
Contoh soal :
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. Tentukanlah jarak :
a. titik D ke garis BF
b. titik B ke garis EG
Penyelesaian :
a. Agar lebih mudah dalam menghitungnya, perhatikan baik - baik gambar kubus berikut ini :
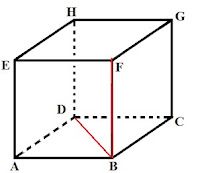
Berdasarkan gambar di atas terlihat bahwa jarak titik D ke garis BF adalah panjang diagonal BD yang bisa ditentukan dengan menggunakan teorema phytagoras ataupun menggunakan rumus.
BD2 = AB2 + AD2
= 42 + 42
= 32
BD = √32
= 4√2
Jika kita menggunakan rumus, maka hasilnya akan seperti di bawah ini :
d = s√2
BD = AB√2
= (4 cm)√2
= 4√2 cm
Jadi, jarak titik D ke garis BF adalah 4√2 cm.
b. Penyelesaiannya sama dengan soal a kita harus membuat gambarnya terlebih dahulu sebelum menguraikan jawaban agar lebih mudah mengerjakannya.

Dari penyelesaian soal a telah diketahui panjang diagonal sisi kubus FH = BD adalah 4√2 cm.
Untuk menentukan panjang BP, kita harus menggunakan teorema phytagoras untuk segitiga siku - siku BFP, sehingga :
FP = 1/2 FH = 2√2
Maka :
BP2 = FP2 + BF2
= (2√2)2 + 42
= 8 + 16
= 24
BP = √24
= 2√6 cm
Jadi, jarak titik B ke garis EG adalah 2√6 cm.
Demikinlah pembahasan materi mengenai Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus. Semoga kalian bisa memahami pembahasan contoh soal di atas sehingga artikel ini bisa membantu kalian dalam menyelesaikan soal - soal yang berkaitan dengan materi yang disampaikan kali ini.
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus Lengkap
Rangkuman Materi Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus Lengkap
Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus - Materi kali ini akan membahas khusus tentang pembahasan contoh soal dalam menghitung jarak titik ke garis pada bangun ruang kubus. Untuk lebih jelasnya langsung saja kita masuk ke pembahasan contoh soal.Contoh soal :
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. Tentukanlah jarak :
a. titik D ke garis BF
b. titik B ke garis EG
Penyelesaian :
a. Agar lebih mudah dalam menghitungnya, perhatikan baik - baik gambar kubus berikut ini :

Berdasarkan gambar di atas terlihat bahwa jarak titik D ke garis BF adalah panjang diagonal BD yang bisa ditentukan dengan menggunakan teorema phytagoras ataupun menggunakan rumus.
BD2 = AB2 + AD2
= 42 + 42
= 32
BD = √32
= 4√2
Jika kita menggunakan rumus, maka hasilnya akan seperti di bawah ini :
d = s√2
BD = AB√2
= (4 cm)√2
= 4√2 cm
Jadi, jarak titik D ke garis BF adalah 4√2 cm.
b. Penyelesaiannya sama dengan soal a kita harus membuat gambarnya terlebih dahulu sebelum menguraikan jawaban agar lebih mudah mengerjakannya.

Dari penyelesaian soal a telah diketahui panjang diagonal sisi kubus FH = BD adalah 4√2 cm.
Untuk menentukan panjang BP, kita harus menggunakan teorema phytagoras untuk segitiga siku - siku BFP, sehingga :
FP = 1/2 FH = 2√2
Maka :
BP2 = FP2 + BF2
= (2√2)2 + 42
= 8 + 16
= 24
BP = √24
= 2√6 cm
Jadi, jarak titik B ke garis EG adalah 2√6 cm.
Demikinlah pembahasan materi mengenai Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus. Semoga kalian bisa memahami pembahasan contoh soal di atas sehingga artikel ini bisa membantu kalian dalam menyelesaikan soal - soal yang berkaitan dengan materi yang disampaikan kali ini.