Rangkuman Materi Kesebangun dan Kekongruenan Bangun datar Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Kesebangun dan Kekongruenan Bangun datar Matematika Dilengkapi Pembahasan Contoh Soal Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Kesebangun dan Kekongruenan Bangun datar Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Kesebangun dan kekongruen biassanya digunakan untuk membandingkan dua buah bangun datar atau lebih dalam bentuk yang sama. Dua buah bangun datar dikatakan sebangun jika panjang setiap sisi pada kedua bangun datar tersebut memiliki nilai perbandingan yang sama. Sedangkan kongruen memiliki konsep yang lebih mendetail. Jika dua buah atau lebih bangun datar memiliki bentuk, ukuran, serta besar sudut yang sama barulah bisa dikatakan sebagai bangun datar yang kongruen.
Perhatikan Gambar di bawah ini :

Perhatikan gambar dua buah persegi panjang berikut ini :
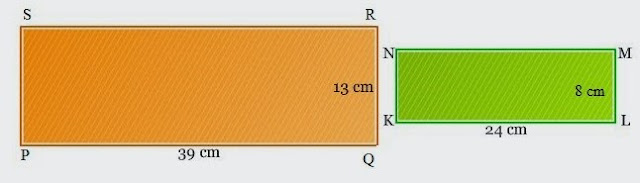
Kedua persegi panjang tersebut merupakan bangun datar yang sebangun karena memiliki kesamaan sifat yang dijelaskan sebagai berikut :
1. Perbandingan antara sisi terpanjang dengan sisi terpendek memiliki nilai yang sama.
=> Perbandingan sisi terpanjang PQ dengan sisi terpendek QR = 39 : 13 = 1 : 3
=> Perbandingan sisi terpanjang KL dengan sisi terpendek LM = 24 : 8 = 1 : 3
=> Perbandingan sisi terpanjang RS dengan sisi terpendek SP = 39 : 13 = 1 : 3
=> Perbandingan sisi terpanjang MN dengan sisi terpendek NK = 24 : 8 = 1 : 3
Dari perhitungan di atas, kita melihat bahwa sisi terpanjang dan terpendek pada kedua persegi panjang tersebut memiliki perbandingan yang sama yaitu 1 : 3.
2. Besar sudut kedua persegi panjang tersebut memiliki nilai yang sama
Sudut P = Sudut K
Sudut Q = Sudut L
Sudut R = Sudut M
Sudut S = Sudut N
Kedua persegi panjang di atas tidak bisa dikatakan sebagai kongruen karena kedua bangun datar tersebut hanya memiliki bentuk dan sudut yang sama besar tetapi tidak memiliki ukuran yang sama.
Penyelesaian :
Karena kedua persegi panjang tersebut sebangun, maka berlaku rumus :
AB / KL = BC / LM
8 / 16 = 5 / LM
LM = 16 x 5 / 8
= 80 / 8
= 10
Jadi, lebar persegi panjang KLMN adalah 10 cm.
Contoh segitiga sebangun :
 Segitiga di atas merupakan segitiga yang sebangun karena perbandingan dari masing - masing sisi memiliki nilai yang sama besar :
Segitiga di atas merupakan segitiga yang sebangun karena perbandingan dari masing - masing sisi memiliki nilai yang sama besar :
Sisi AC sesuai dengan sisi PR = AC / PR = 4 / 2 = 2 / 1
Sisi AB sesuai dengan sisi PQ = AB / PQ = 8 / 4 = 2 / 1
Sisi BC sesuai dengan sisi QR = BC / QR = 6 / 3 = 2 / 1
Maka AC / PR = AB / PQ = BC / QR = 2 / 1
Besar sudut yang bersesuaian memiliki besar yang sama, yaitu :
Sudut A = Sudut P
Sudut B = Sudut Q
Sudut C = Sudut R
 Penyelesaian :
Penyelesaian :
AB / KL = BC / LM
18 / 6 = 15 / LM
3 = 15 / LM
LM = 15 / 3
= 5 cm
Dari hasil tersebut kita bisa mengetahui bahwa perbandingan kedua sisi segitiga di atas adalah :
18 : 6 = 3 : 1
15 : 5 = 3 : 1
12 : MK = 3 : 1
MK = 12 / 3
= 4 cm
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Kesebangun dan Kekongruenan Bangun datar Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Rangkuman Materi Kesebangun dan Kekongruenan Bangun datar Matematika Dilengkapi Pembahasan Contoh Soal Lengkap
Kesebangun dan Kekongruenan Bangun Datar Matematika mempunyai konsep yang cukup sederhana, akan tetapi terkadang kita sering terbalik mendefinisikan keduanya apalagi jika kita memahaminya dengan baik. Untuk lebih memahami materi ini perhatikan baik - baik penjelasan di bawah ini.Kesebangun dan kekongruen biassanya digunakan untuk membandingkan dua buah bangun datar atau lebih dalam bentuk yang sama. Dua buah bangun datar dikatakan sebangun jika panjang setiap sisi pada kedua bangun datar tersebut memiliki nilai perbandingan yang sama. Sedangkan kongruen memiliki konsep yang lebih mendetail. Jika dua buah atau lebih bangun datar memiliki bentuk, ukuran, serta besar sudut yang sama barulah bisa dikatakan sebagai bangun datar yang kongruen.
Perhatikan Gambar di bawah ini :

Kesebangunan dan Kekongruenan Bangun Datar Matematika
Kesebangunan Pada Persegi Panjang
Perhatikan gambar dua buah persegi panjang berikut ini :

Kedua persegi panjang tersebut merupakan bangun datar yang sebangun karena memiliki kesamaan sifat yang dijelaskan sebagai berikut :
1. Perbandingan antara sisi terpanjang dengan sisi terpendek memiliki nilai yang sama.
=> Perbandingan sisi terpanjang PQ dengan sisi terpendek QR = 39 : 13 = 1 : 3
=> Perbandingan sisi terpanjang KL dengan sisi terpendek LM = 24 : 8 = 1 : 3
=> Perbandingan sisi terpanjang RS dengan sisi terpendek SP = 39 : 13 = 1 : 3
=> Perbandingan sisi terpanjang MN dengan sisi terpendek NK = 24 : 8 = 1 : 3
Dari perhitungan di atas, kita melihat bahwa sisi terpanjang dan terpendek pada kedua persegi panjang tersebut memiliki perbandingan yang sama yaitu 1 : 3.
2. Besar sudut kedua persegi panjang tersebut memiliki nilai yang sama
Sudut P = Sudut K
Sudut Q = Sudut L
Sudut R = Sudut M
Sudut S = Sudut N
Kedua persegi panjang di atas tidak bisa dikatakan sebagai kongruen karena kedua bangun datar tersebut hanya memiliki bentuk dan sudut yang sama besar tetapi tidak memiliki ukuran yang sama.
Contoh Soal Kesebangun pada Persegi Panjang
Dua buah persegi panjang memiliki ukuran yang berbeda yakni ABCD dan KLMN. Persegi panjang ABCD memiliki panjang 8 cm dan lebar 5 cm. Jika diketahui persegi panjang ABCD sebangun dengan persegi panjang KLMN yang memiliki panjang 16 cm, maka tentukan lebar persegi panjang KLMN !Penyelesaian :
Karena kedua persegi panjang tersebut sebangun, maka berlaku rumus :
AB / KL = BC / LM
8 / 16 = 5 / LM
LM = 16 x 5 / 8
= 80 / 8
= 10
Jadi, lebar persegi panjang KLMN adalah 10 cm.
Kesebangunan pada Segitiga
Kesebangunan pada segitiga sedikit lebih sulit diketahui karena terdapat tiga buah sisi yang harus sama perbandingannya.Contoh segitiga sebangun :

Sisi AC sesuai dengan sisi PR = AC / PR = 4 / 2 = 2 / 1
Sisi AB sesuai dengan sisi PQ = AB / PQ = 8 / 4 = 2 / 1
Sisi BC sesuai dengan sisi QR = BC / QR = 6 / 3 = 2 / 1
Maka AC / PR = AB / PQ = BC / QR = 2 / 1
Besar sudut yang bersesuaian memiliki besar yang sama, yaitu :
Sudut A = Sudut P
Sudut B = Sudut Q
Sudut C = Sudut R
Contoh Soal Kesebangunan pada Segitiga
Diketahui sebuah segitiga ABC sebangun dengan segitiga KLM. Tentukanlah panjang LM dan MK berdasarkan gambar di bawah ini :
AB / KL = BC / LM
18 / 6 = 15 / LM
3 = 15 / LM
LM = 15 / 3
= 5 cm
Dari hasil tersebut kita bisa mengetahui bahwa perbandingan kedua sisi segitiga di atas adalah :
18 : 6 = 3 : 1
15 : 5 = 3 : 1
12 : MK = 3 : 1
MK = 12 / 3
= 4 cm