Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap
Perhatikan gambar segitiga pascal berikut ini :
Dari gambar segitiga pascal di atas, bisa kita lihat bahwa puncak bagian teratas baris ke - 0 diisi dengan angka 1. Kemudian di bawahnya (baris ke - 1) diisi dengan angka 1 dan 1. Kemudian baris selanjutnya (baris ke - 2) masih diisi dengan angka 1 dan 1 dibagian sisinya kemudian pada bagian dalam diisi dengan hasil dari penjumlahan dua bilangan yang ada di atasnya yaitu 1+1=2.
merupakan koefisien dari setiap baris segitiga pascal, yang apabila dijabarkan maka akan terlihat bahwa koefisien yang diperoleh dari bentuk tersebut sama persis dengan bilangan yang ada pada setiap baris segitiga pascal di atas.
Untuk lebih jelasnya perhatikan bentuk penyederhanaan berikut :
1. (a + b)1 = a + b → Koefisiennya adalah 1 dan 1
2. (a + b)2 = a2 + 2ab + b2 → Koefisiennya adalah 1, 2, dan 1
3. (a + b)3 = (a + b) (a2 +2ab + b2)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3
= a3 + 3a2b + 3ab2 + b3 → Koefisiennya adalah 1, 3, 3, dan 1
Semua bilangan di atas merupakan koefisien dari expansi pangkat binomial,
Perhatikan contoh berikut :
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
dari contoh tersebut, pada i = 4 diperoleh koefisien dari expansi pangkat binomial 4 yaitu 1, 4, 6, 4, dan 1 yang merupakan bilangan - bilangan yang mengisi baris ke - 4 pada segitiga pascal.
Perhatikan teorema binomial berikut :
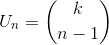
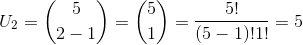
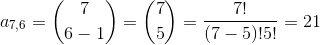
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap
Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap
Rumus Segitiga Pascal dalam Matematika - Segitiga pascal merupakan sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga. Manfaat dari segitiga pascal ini salah satunya yaitu untuk menyelesaikan soal perpangkatan dengan cepat, dari segitiga pascal ini kita tidak perlu mengalikan bilangan satu persatu tetapi bisa langsung mengetahui koefisien dari penyelesaian soal perpangkatan.Perhatikan gambar segitiga pascal berikut ini :
 |
| Lima barisan pertama pada segitiga pascal |
Untuk baris ke - 3 diisi dengan angka 1 dan 1 pada bagian sisi kemudian bagian tengahnya diisi dengan hasil dari penjumlahan dua bilangan yang ada pada baris ke - 2 yaitu 1+2=3. Kemudian baris keempat (angka 4) dihasilkan dari penjumlahan dua bilangan yang ada di atasnya, yaitu 1+3=4 begitu juga angka 6 dihasilkan dari penjumlahan dua bilangan yang ada di atasnya yaitu 3+3=6, dan seterusnya.
Rumus Segitiga Pascal
Penyederhanaan bentuk merupakan koefisien dari setiap baris segitiga pascal, yang apabila dijabarkan maka akan terlihat bahwa koefisien yang diperoleh dari bentuk tersebut sama persis dengan bilangan yang ada pada setiap baris segitiga pascal di atas.Untuk lebih jelasnya perhatikan bentuk penyederhanaan berikut :
1. (a + b)1 = a + b → Koefisiennya adalah 1 dan 1
2. (a + b)2 = a2 + 2ab + b2 → Koefisiennya adalah 1, 2, dan 1
3. (a + b)3 = (a + b) (a2 +2ab + b2)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3
= a3 + 3a2b + 3ab2 + b3 → Koefisiennya adalah 1, 3, 3, dan 1
Semua bilangan di atas merupakan koefisien dari expansi pangkat binomial,
Perhatikan contoh berikut :
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
dari contoh tersebut, pada i = 4 diperoleh koefisien dari expansi pangkat binomial 4 yaitu 1, 4, 6, 4, dan 1 yang merupakan bilangan - bilangan yang mengisi baris ke - 4 pada segitiga pascal.
Perhatikan teorema binomial berikut :
Dari uraian di atas, secara umum bisa disimpulkan bahwa barisan bilangan pada baris i = k dalam segitiga pascal dapat dituliskan menjadi :
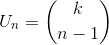
Lebih jelasnya, kita ambil contoh dari bilangan ke - 2 dan ke - 3 pada baris ke - 5 dalam segitiga pascal, sehingga :
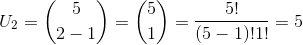
Berdasarkan pola di atas diperoleh rumus baru yang bisa digunakan untuk menentukan bilangan ai,j yang merupakan bilangan pada baris ke - i dan kolom ke - j, seperti di bawah ini :
Kemudian, misalkan kita akan mencari bilangan baris ke - 7 tepat pada kolom ke - 6, maka rumusnya :
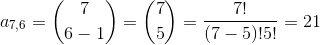
Dari penjabaran rumus di atas, barisan bilangan ke - d dapa dituliskan sebagai berikut :
Sebagai pembuktian dari rumus di atas, kita coba mencari diagonal ke - 3 yang memiliki pola n(n + 1) / 2 dalam segitiga pascal dengan d = 3, sehingga :
Demikianlah penjelasan materi tentang Rumus Segitiga Pascal dalam Matematika, semoga kalian bisa memahami materi ini dengan mudah sehingga bisa membantu kalian dalam mengerjakan soal - soal. Selamat belajar.