Rangkuman Materi Persamaan Nilai Mutlak dan Cara Penyelesaiannya Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Persamaan Nilai Mutlak dan Cara Penyelesaiannya Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Persamaan Nilai Mutlak dan Cara Penyelesaiannya Lengkap
Konsep di atas bisa diperluas penggunaannya dalam menyelesaikan persoalan yang berkaitan dengan bentuk aljabar yang terletak pada simbol - simbol nilai mutlak. Hal ini dijelaskan oleh sifat persamaan nilai mutlak sebagai berikut :
"Apabila x merupakan sebuah bentuk aljabar, sedangkan n merupakan bilangan riil positif, maka |x| = n bisa diimplikasikan menjadi x = n atau x = -n"
Perlu diketahui bahwa sifat ini hanya bisa diaplikasikan sesudah kita melakukan isolasi terhadap simbol nilai mutlak yang ada pada satu ruas. Untuk lebih mudah memahaminya, perhatikan baik - baik pembahasan contoh soal persamaan nilai mutlak berikut ini :
Contoh Soal 1 :
Tentukanlah persamaan berikut ini :
-3 x -4 + 5 = 14
Penyelesaian :
Langkah pertama kita harus mengisolasi nilai mutlak caranya dengan memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain kita pindahkan menuju ruas yang lain. Sehingga :
-3 |x-4| + 5 = 14
-3 |x-4| = 14 - 5
-3 |x4| = 9
|x-4| = 3
Dalam persamaan nilai mutlak x - 4 adalah "X" sehingga bisa disimpulkan bahwa :
x - 4 = 3 atau x - 4 = -3
sehingga :
x = 7 atau x = 1
Jadi, himpunan penyelesaian dari persamaan tersebut adalah {7, 1}
Contoh Soal 2 :
Tentukan himpunan penyelesaian dari persamaan |4 - 2/5x| - 7 = 13
Penyelesaian :
|4 - 2/5x| - 7 = 13
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Persamaan Nilai Mutlak dan Cara Penyelesaiannya Lengkap
Rangkuman Materi Persamaan Nilai Mutlak dan Cara Penyelesaiannya Lengkap
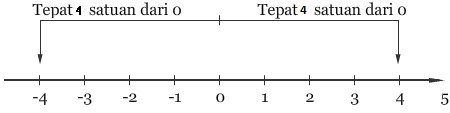
Persamaan Nilai Mutlak - Nilai mutlak sebuah bilangan merupakan jarak bilangan terhadap titik 0 pada garis bilangan tanpa memperhatikan arahnya. Pengertian tersebut kita ambil contoh |x| = 4 mempunyai dua buah penyelesaian dikarenakan ada dua buah bilangan yang jaraknya 4 titik dari 0 yaitu x = 4 dan x = -4. Hal ini bisa kalian lihat pada gambar berikut ini :
"Apabila x merupakan sebuah bentuk aljabar, sedangkan n merupakan bilangan riil positif, maka |x| = n bisa diimplikasikan menjadi x = n atau x = -n"
Perlu diketahui bahwa sifat ini hanya bisa diaplikasikan sesudah kita melakukan isolasi terhadap simbol nilai mutlak yang ada pada satu ruas. Untuk lebih mudah memahaminya, perhatikan baik - baik pembahasan contoh soal persamaan nilai mutlak berikut ini :
Contoh Soal 1 :
Tentukanlah persamaan berikut ini :
-3 x -4 + 5 = 14
Penyelesaian :
Langkah pertama kita harus mengisolasi nilai mutlak caranya dengan memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain kita pindahkan menuju ruas yang lain. Sehingga :
-3 |x-4| + 5 = 14
-3 |x-4| = 14 - 5
-3 |x4| = 9
|x-4| = 3
Dalam persamaan nilai mutlak x - 4 adalah "X" sehingga bisa disimpulkan bahwa :
x - 4 = 3 atau x - 4 = -3
sehingga :
x = 7 atau x = 1
Jadi, himpunan penyelesaian dari persamaan tersebut adalah {7, 1}
Contoh Soal 2 :
Tentukan himpunan penyelesaian dari persamaan |4 - 2/5x| - 7 = 13
Penyelesaian :
|4 - 2/5x| - 7 = 13
|4 - 2/5x| = 13 + 7
|4 - 2/5x| = 20
maka :
|4 - 2/5x| = 20 atau |4 - 2/5x| = -20
|4 - 2/5x| = 20
maka :
|4 - 2/5x| = 20 atau |4 - 2/5x| = -20
sehingga :
-2/5x = 16
x = 16 x 5 : -2
= 80 : -40
atau
-2/5x = -24
x = -24 x 5 : -2
= -120 : -2
= 60
Jadi, himpunan penyelesaiannya adalah {-40, 60}
Demikianlah pembahasan materi mengenai Persamaan Nilai Mutlak dan Cara Penyelesaiannya. Semoga kalian bisa memahami penjelasan dan contoh soal di atas dengan mudah sehingga artikel ini dapat membantu kalian dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar!