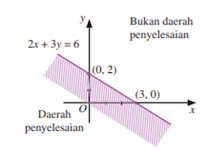
Daerah Himpunan Pertidaksamaan Linear Dua Variabel Dengan Grafik

A. Pertidaksamaan linear dua variabel Pertidaksamaan linear dua variabel adalah suatu pertidaksamaan yang didalamnya memuat dua variabel yang masing-masing variabel berderajat satu dan tidak terjadi perkalian antar variabelnya....

Langkah-Langkah Menentukan Nilai Optimum Program Linear SMA

Program linear merupakan salah satu ilmu matematika yang digunakan untuk memaksimumkan atau meminimumkan fungsi objektif dengan kendala tertentu. Untuk menentukan suatu nilai optimum (maksimum / minimum) pada permasalahan program...

Pengertian Program Linear Kelas XI MIA SMA

Program linear merupakan salah satu ilmu matematika yang digunakan untuk memaksimumkan atau meminimumkan fungsi objektif dengan kendala tertentu. Dalam kehidupan sehari-hari sering ditemukan berbagai persoalan yang berkaitan dengan...

Cara Menyelesaikan SPLDV Dengan Metode Grafik

Sistem Persamaan Linier Dua Variabel adalah suatu sistem persamaan yang variabel-variabel dari persamaan tersebut berpangkat satu. Sistem persamaan liner dua variabel terdiri atas dua persamaan linier yang masing-masing bervariabel...

Cara Menyelesaikan SPLDV Dengan Metode Substitusi - Eliminasi

Menyelesaikan SPLDV Dengan Metode Sustitusi - Eliminasi A. Metode Substitusi Penyelesaian  menggunakan metode substitusi dilakukan dengan cara menyatakan salah satu variabel dalam bentuk variabel yang lain kemudian nilai...