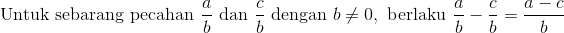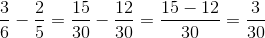Matematika Rumus Bangun Ruang dan Bangun Datar
pada October 14, 2016
RUMUS-RUMUS BANGUN RUANG DAN BANGUN DATAR
A. RUMUS BANGUN RUANG

a. Kubus
Rumus:
· Luas permukaan: 6 x s2 =6s2
· Volume: s x s x s= s3

b. Balok
Rumus:
· Luas permukaan: 2{(p x l)+(p x t)+(l x t)}
· Volume: p x l x t

c. Limas
Rumus:
· Luas permukaan: La + jumlah luas segitiga pada bidang tegak
· Volume : 1/3 x La x t
La=luas alas
t= tinggi

d. Prisma
Rumus:
· Luas permukaan : (2 x La)+(K x t)
· Volume: La x t
La= luas alas
K= keliling alas
t= tinggi

e. Tabung
Rumus:
· Luas permukaan: 2 π r (r+t)
· Luas selimut: 2 π r t
· Volume : π r2 t
π= 22/7 atu 3,14
r= jari-jari alas
t= tinggi tabung

f. Kerucut
Rumus:
· Luas permukaan: π r (r+s)
· Luas selimut: π r s
· Volume: 1/3 π r2 t
r= jari-jari lingkaran alas
s= panjang garis pelukis kerucut
t= tinggi kerucut

g. Bola
Rumus :
· Luas permukaan: 4 π r2
· Volume: 4/3 π r3
r= jari-jari bola
B. Macam Macam Rumus Bangun Datar dan Sifatnya
Bangun Datar terdiri dari segitiga, persegi, persegi panjang, jajaran genjang, belah ketupat, layang layang, trapesi
Berikut saya akan berbagi info tentang bangun datar berdasarkan definisi bangun datar, sifat sifat bangun datar, rumus keliling dan rumus luas

SEGITIGA
Definisi:
Segitiga adalah bangun geometri yang dibuat dari tiga sisi yang berupa garis lurus dan tiga sudut.
Sifat-Sifat:
Jumlah sudut pada segitiga besarnya 180⁰.
Jenis-jenis segitiga :
1) Segitiga Sama Sisi
a. mempunyai 3 simetri lipat.
b. mempunyai 3 simetri putar.
c. mempunyai 3 sisi sama panjang.
d. mempunyai 3 sudut sama besar yaitu 60⁰.
2) Segitiga Sama Kaki
a. mempunyai 1 simetri lipat.
b. mempunyai 1 simetri putar.
c. mempunyai 2 sisi yang berhadapan sama panjang.
3) Segitiga Siku-Siku
a. tidak mempunyai simetri lipat dan simetri putar.
b. mempunyai 2 sisi yang saling tegak lurus.
c. mempunyai 1 sisi miring.
d. salah satu sudutnya adalah sudut siku-siku yaitu 90⁰.
e. untuk mencari panjang sisi miring digunakan rumus phytagoras :

PERSEGI
Definisi:
Persegi adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang dan memiliki empat buah sudut siku-siku.
Sifat:
Mempunyai 4 titik sudut.
Mempunyai 4 sudut siku-siku 90⁰.
Mempunyai 2 diagonal yang sama panjang.
Mempunyai 4 simetri lipat.
Mempunyai 4 simetri putar.

PERSEGI PANJANG
Definisi:
Persegi panjang adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki empat buah sudut siku-siku.
Sifat Sifat:
Sisi yang berhadapan sama panjang dan sejajar.
Sisi-sisi persegi panjang saling tegak lurus
Mempunyai 4 sudut siku-siku 90⁰.
Mempunyai 2 diagonal yang sama panjang
Mempunyai 2 simetri lipat.
Mempunyai 2 simetri putar

JAJARAN GENJANG
Definisi:
Jajaran Genjang adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki dua pasang sudut bukan siku-siku yang masing-masing sama besar dengan sudut di hadapannya.
Sifat-Sifat:
Tidak mempunyai simetri lipat dan simetri putar.
Sisi yang berhadapan sejajar dan sama panjang.
Dua sisi lainnya tidak saling tegak lurus.
Mempunyai 4 sudut, 2 sudut berpasangan dan berhadapan.
Sudut yang saling berdekatan besarnya 180⁰.
Mempunyai 2 diagonal yang tidak sama panjang.

BELAH KETUPAT
Definisi:
Belah ketupat adalah bangun datar dua dimensi yang dibentuk oleh empat rusuk yang sama panjang dan dan memiliki dua pasang sudut bukan siku-siku yang masing-masing sama besar dengan sudut di hadapannya.
Sifat- Sifat:
Mempunyai 2 simetri lipat.
Mempunyai 2 simeteri putar.
Mempunyai 4 titik sudut.
Sudut yang berhadapan besarnya sama.
Sisinya tidak tegak lurus.
Mempunyai 2 diagonal yang berbeda panjangnya.

LAYANG-LAYANG
Definisi:
Layang-layang adalah bangun geometri berbentuk segiempat yang terbentuk dari dua segitiga sama kaki yang alasnya berhimpitan.
Sifat-Sifat:
Mempunyai 1 simetri lipat. Tidak mempunyai simetri putar
Mempunyai 4 sisi sepasang-sepasang yang sama panjang.
Mempunyai 4 buah sudut.
Sepasang sudut yang berhadapan sama besar.
Mempunyai 2 diagonal berbeda dan tegak lurus.

TRAPESIUM
Definisi:
Trapesium adalah bangun segiempat dengan sepasang sisi berhadapan sejajar.
Sifat-Sifat:
Tiap pasang sudut yang sisinya sejajar adalah 180⁰.
Jenis-jenis trapesium:
a. Trapesium Sembarang
mempunyai sisi-sisi yang berbeda.
b. Trapesium Siku-SIku
mempunyai sudut siku-siku.
c. Trapesium Sama Kaki
mempunyai sepasang kaki sama panjang

LINGKARAN
Definisi:
Lingkaran merupakan kurva tertutup sederhana beraturan.
Sifat-Sifat
Jumlah derajat lingkaran sebesar 360⁰.
Lingkaran mempunyai 1 titik pusat.
Mempunyai simetri lipat dan simetri putar yang jumlahnya tidak terhingga.
Istilah-istilah dalam lingkaran :
a. Diameter lingkaran (d) yaitu ruas garis yang menghubungkan dua titik pada busur lingkaran melalui titik pusat lingkaran.
b. Jari-jari lingkaran (r) yaitu ruas garis yang menghubungkan titik pada busur lingkaran dengan titik pusat lingkaran.
c. Tali busur yaitu garis yang menghubungkan dua titik pada busur lingkaran dan tidak melewati titik pusat lingkaran.
d. Busur yaitu bagian lingkaran yang dibagi oleh tali busur.
e. Juring yaitu daerah pada lingkaran yang dibatasi oleh 2 jari-jari maupun busur lingkaran.
f. Susut pusat yaitu sudut yang dibentuk oleh 2 buah jari-jari.







 (Jumlahkan bilangan pecahan dengan bilangan pecahan)
(Jumlahkan bilangan pecahan dengan bilangan pecahan)