Rangkuman Materi Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya Lengkap
Garis Tinggi (altitude)
Garis tinggi merupakan sebuah garis tegak lurus yang ditarik dari salah satu titik sudut segitiga menuju sisi yang ada di hadapannya.
Perhatikan gambar di bawah ini :

Pada gambar segitiga di atas, putus - putus yang menghubungkan titik C dan D adalah garis tinggi dimana alasnya merupakan garis AB. Akan tetapi, garis tinggi tidak selamanya muncul pada garis AB. Sebagai contoh, dalam sebuah segitiga tumpul, garis tinggi biasanya didapat dengan menggambar perpanjangan dari garis AB tersebut. Perhatikan gambar berikut ini :
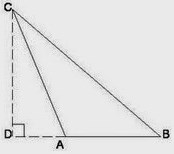
Panjang garis tinggi bisa diketahui dengan cara menghitung luas segitiganya terlebih dahulu dengan menggunakan rumus luas segitiga (1/2 x alas x tinggi). Dengan rumus tersebut kita bisa mengetahui tinggi sebuah segitiga. Perhatikan baik - baik pembahasan di bawah ini :
Dalam segitiga PQR berikut ini, panjang PQ adalah 24 cm, panjang QR adalah 20 cm dan panjang PS adalah 16 cm. Maka, berapakah panjang RT?

Penyelesaian :
Dari segitiga tersebut kita bisa mengetahui bahwa : luas segitiga dengan alas PQ = luas segitiga dengan alas QR. Maka cara menghitungnya adalah :
1/2 x PQ x PS = 1/2 x QR x RT
1/2 x 24 x 16 = 1/2 x 20 x RT
24 x 16 = 20 x RT
384 = 20 RT
RT = 384 / 20
= 19,2 cm

Jika kita menarik tiga buah garis berat pada segitiga. Maka garis berat tersebut akan saling berpotongan pada sebuah titik pusat. Titik pusat ini dinamakan sebagai centroid dimana pada titik inilah segitiga tersebut bisa meraih kesetimbangan.

Keistimewaan dari garis berat yang muncul pada segitiga adalah garis - garis berat tersebut akan selalu berpotongan dengan persentasi perbandingan 2 : 1
Panjang garis berat bisa diketahui dengan menggunakan rumus :

Untuk memahami rumus tersebut, perhatikan baik - baik contoh soal dan pembahasan di bawah ini :
Sebuah segitiga DEF, FG merupakan sebuah garis berat dimana DE = 12 cm, EF = 8 cm, dan DF = 10 cm. Maka berapakah panjang FG ?
Penyelesaian :
FG2 = 1/2 x 82 + 1/2 x 102 - 1/4 x 122
= 1/2 x 64 + 1/2 x 100 - 1/4 x 144
= 32 + 50 - 36
= 82 - 36
= 46
Panjang garis bagi dalam bisa diketahui dengan menggunakan perhitungan rumus :


Panjang garis bagi luar bisa diketahui dengan menggunakan perhitungan rumus :

Garis sumbu merupakan sebuah garis yang melintas pada titik tengah dari sebuah segitiga dan posisinya tegak lurus terhadap sisi tersebut. Apabila tiga buah garis sumbu ditarik dari setiap sisi segitiga maka mereka akan bertemu pada sebuah titik yang disebut dengan circumcenter. Apabila kita menggambar sebuah lingkaran dari titik sudut yang ada pada segitiga, maka circumcenter menjadi titik pusat dari lingkaran tersebut. Perhatikan gambar di bawah ini :

Demikianlah pembahasan materi mengenai Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya. Semoga kalian bisa memahami penjelasan di atas dengan mudah sehingga artikel ini bisa membantu kalian dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar dan semoga bermanfaat!
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya Lengkap
Rangkuman Materi Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya Lengkap
Belajar Matematikaku - Dalam artikel kali ini akan membahas materi mengenai Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya. Pada segitiga terdapat 4 jenis garis istimewa yaitu garis tinggi atau altitude, garis berat atau median, garis bagi atau angle bisector, dan garis sumbu atau perpendicular bisector. Dari setiap jenis garis istimewa tersebut mempunyai pengertian tersendiri. Berikut pembahasan mengenai garis - garis istimewa tersebut beserta contoh soal.Pengertian Garis Istimewa Pada Segitiga dan Rumus Cara Menghitungnya
Garis Tinggi (altitude)
Garis tinggi merupakan sebuah garis tegak lurus yang ditarik dari salah satu titik sudut segitiga menuju sisi yang ada di hadapannya.
Perhatikan gambar di bawah ini :

Pada gambar segitiga di atas, putus - putus yang menghubungkan titik C dan D adalah garis tinggi dimana alasnya merupakan garis AB. Akan tetapi, garis tinggi tidak selamanya muncul pada garis AB. Sebagai contoh, dalam sebuah segitiga tumpul, garis tinggi biasanya didapat dengan menggambar perpanjangan dari garis AB tersebut. Perhatikan gambar berikut ini :

Panjang garis tinggi bisa diketahui dengan cara menghitung luas segitiganya terlebih dahulu dengan menggunakan rumus luas segitiga (1/2 x alas x tinggi). Dengan rumus tersebut kita bisa mengetahui tinggi sebuah segitiga. Perhatikan baik - baik pembahasan di bawah ini :
Dalam segitiga PQR berikut ini, panjang PQ adalah 24 cm, panjang QR adalah 20 cm dan panjang PS adalah 16 cm. Maka, berapakah panjang RT?

Penyelesaian :
Dari segitiga tersebut kita bisa mengetahui bahwa : luas segitiga dengan alas PQ = luas segitiga dengan alas QR. Maka cara menghitungnya adalah :
1/2 x PQ x PS = 1/2 x QR x RT
1/2 x 24 x 16 = 1/2 x 20 x RT
24 x 16 = 20 x RT
384 = 20 RT
RT = 384 / 20
= 19,2 cm
Garis Berat (median)
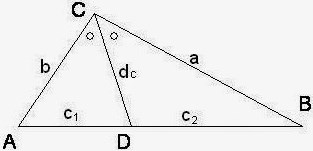
Garis berat merupakan sebuah garis yang ditarik dari salah satu titik yang ada pada segitiga menuju ke sebuah titik tengah pada sisi yang berlawanan. Dengan menarik sebuah garis berat pada sisi yang berlawanan. Dengan menarik sebuah garis berat pada segitiga akan menghasilkan dua buah segitiga yang sama luas. Perhatikan gambar segitiga berikut ini. Dengan menarik garis berat CD maka akan terbentuk dua buah segitiga ACD dan BCD yang sama luasnya.
Jika kita menarik tiga buah garis berat pada segitiga. Maka garis berat tersebut akan saling berpotongan pada sebuah titik pusat. Titik pusat ini dinamakan sebagai centroid dimana pada titik inilah segitiga tersebut bisa meraih kesetimbangan.

Keistimewaan dari garis berat yang muncul pada segitiga adalah garis - garis berat tersebut akan selalu berpotongan dengan persentasi perbandingan 2 : 1
Panjang garis berat bisa diketahui dengan menggunakan rumus :

Untuk memahami rumus tersebut, perhatikan baik - baik contoh soal dan pembahasan di bawah ini :
Sebuah segitiga DEF, FG merupakan sebuah garis berat dimana DE = 12 cm, EF = 8 cm, dan DF = 10 cm. Maka berapakah panjang FG ?
Penyelesaian :
FG2 = 1/2 x 82 + 1/2 x 102 - 1/4 x 122
= 1/2 x 64 + 1/2 x 100 - 1/4 x 144
= 32 + 50 - 36
= 82 - 36
= 46
FG = √46 cm.
Garis Bagi Dalam
Garis bagi dalam merupakan sebuah garis yang ditarik dari salah satu titik pada segitiga dan berfungsi membagi dua buah sudut yang ada disebelah garis tersebut menjadi sama besar. Garis tersebut terletak di dalam segitiga :
Panjang garis bagi dalam bisa diketahui dengan menggunakan perhitungan rumus :

Garis Bagi Luar
Garis bagi luar pada segitiga merupakan sebuah garis yang ditarik dari salah satu sudut pada segitiga dan membagi dua buah sudut yang sama besar pada salah satu sisi segitiga dengan perpanjangan dari salah satu garis sisi yang lain. Garis tersebut terletak di bagian luar segitiga.
Panjang garis bagi luar bisa diketahui dengan menggunakan perhitungan rumus :

Garis Sumbu (perpendicular bisector)
Garis sumbu merupakan sebuah garis yang melintas pada titik tengah dari sebuah segitiga dan posisinya tegak lurus terhadap sisi tersebut. Apabila tiga buah garis sumbu ditarik dari setiap sisi segitiga maka mereka akan bertemu pada sebuah titik yang disebut dengan circumcenter. Apabila kita menggambar sebuah lingkaran dari titik sudut yang ada pada segitiga, maka circumcenter menjadi titik pusat dari lingkaran tersebut. Perhatikan gambar di bawah ini :
Demikianlah pembahasan materi mengenai Garis Istimewa pada Segitiga dan Rumus Cara Menghitungnya. Semoga kalian bisa memahami penjelasan di atas dengan mudah sehingga artikel ini bisa membantu kalian dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar dan semoga bermanfaat!