Rangkuman Materi Pengertian, Rumus, dan Contoh Bilangan Pangkat Pecahan Lengkap
Selamat datang bagi teman - teman di Materi Matematika, Pada kesempatan kali ini kami akan berbagi dengan teman teman di manapun kalian berada, tentang materi pelajaran matematika yang kami beri judul Rangkuman Materi Pengertian, Rumus, dan Contoh Bilangan Pangkat Pecahan Lengkap, Semoga pembahasan yang kami tulis ini dapat menjadi acuan kalian semua dalam belajar Matematika .
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Pengertian, Rumus, dan Contoh Bilangan Pangkat Pecahan Lengkap
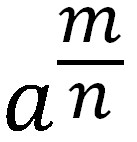
=> Misalkan 16a = 4 jika 16 dipangkatkan dengan a hasilnya adalah 4, maka nilai a adalah :
16a = 4
(42)a = 41
42a = 41
2a =1
a = ½
Sehingga bisa disimpulkan bahwa 161/2 = 4. Karena √16 = 4 maka disimpulkan bahwa √16 = 161/2
=> Misalkan 216x = 6, Maka nilai x adalah :
216x = 6
(63)x = 61
63x = 61
3x = 61
x = 1/3
Jadi, 2161/3 = 6 atau 3√216 = 6
Berdasarkan kedua contoh di atas, maka rumus bilangan berpangkat sederhana bisa ditulis menjadi :
Dengan syarat a ≥ 0 dimana m dan n merupakan bilangan bulat positif.
Mengubahnya Menjadi Operasi Akar
Untuk mengubah bilangan pangkat pecahan menjadi akar, bisa menggunakan rumus :
Misalkan kita ingin menyelesaikan bilangan 272/3
Penyelesaian :
272/3 = 271/3 x 2 = (271/3)2 = (3√27)2 = 32 = 9
Mengubah Bilangan Pokok Menjadi Bilangan Berpangkat Sama Dengan Penyebut Pada Pangkat Pecahan
Dengan menggunakan cara ini kita bisa menyelesaikan soal bilangan berpangkat pecahan tanpa harus mengubahnya terlebih dahulu ke dalam bentuk operasi akar.
Perhatikan baik - baik contoh berikut ini :
43/2 = (22)3/2 = 22x3/2 = 23 = 8
272/3 = (33)2/3 = 33x2/3 = 32 = 9
Untuk memperluas pengetahuan kalian tentang materi ini, pelajari beberapa contoh soal dan pembahasan bilangan pangkat berikut ini :
Pecahan
Contoh Soal 1 :
a. 51/2
b. 63/2
c. 127/2
Penyelesaian :
a. 51/2 = √5
b. 63/2 = √63
c. 127/2 = √127
Contoh Soal 2 :
Sederhanakanlah bentuk - bentuk pecahan berikut ini :
a. 65/2 x 63/2
b. 31/2 x 31/2
c. (45/2)3/5
Penyelesaian :
a. 65/2 x 63/2 = 6(5/2) + (3/2) = 68/2 = 64 = 1296
b. 31/2 x 31/2 = 3(1/2) + (1/2) = 31 = 3
c. (45/2)3/5 = 4(5/2 x 3/5) = 415/10 = 43/2
Hubungan antar garis limit fungsi bunga pertumbuhan dan peluruhan bilangan bulat berpangkat barisan deret bangun datar ruang sisi lengkung bola cos kombinasi contoh soal yang cocok untuk pendekatan scientific open ended tes cerdas cermat statistika counting sin tan cacah model pembelajaran jigsaw pbl cerita tentang cosinus sbmptn dimensi tiga. Namun yang akan kita bahas pada kesempatan kali ini adalah Rangkuman Materi Pengertian, Rumus, dan Contoh Bilangan Pangkat Pecahan Lengkap
Rangkuman Materi Pengertian, Rumus, dan Contoh Bilangan Pangkat Pecahan Lengkap
Bilangan Pangkat Pecahan - Untuk memahami materi ini terlebih dahulu kalian harus memahami materi tentang Pengertian, Operasi, Rumus dan Sifat - Sifat Bilangan Berpangkat yang telah disampaikan pada pembahasan sebelumnya. Dalam materi sebelumnya telah dijelaskan bahwa bilangan berpangkat positif an (a pangkat n) yang mana merupakan perkalian bilangan a secara berulang sebanyak n faktor. Contoh, 32 = 3 x 3. Sementara untuk bilangan pangkat pecahan ada cara - cara tersendiri dalam menyelesaikan soal dalam bentuk bilangan pangkat pecahan. Untuk lebih memahami materi ini, perhatikan baik - baik penjelasan di bawah ini.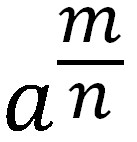
Rumus dan Contoh Bilangan Pangkat Pecahan
Langsung saja mengenai pembahasan contoh soal :=> Misalkan 16a = 4 jika 16 dipangkatkan dengan a hasilnya adalah 4, maka nilai a adalah :
16a = 4
(42)a = 41
42a = 41
2a =1
a = ½
Sehingga bisa disimpulkan bahwa 161/2 = 4. Karena √16 = 4 maka disimpulkan bahwa √16 = 161/2
=> Misalkan 216x = 6, Maka nilai x adalah :
216x = 6
(63)x = 61
63x = 61
3x = 61
x = 1/3
Jadi, 2161/3 = 6 atau 3√216 = 6
Berdasarkan kedua contoh di atas, maka rumus bilangan berpangkat sederhana bisa ditulis menjadi :
am/n = n√am
Cara Menyelesaikan Soal Bilangan Berpangkat
Ada beberapa cara yang bisa kita lakukan dalam menyelesaikan soal - soal mengenai bilangan berpangkat, diantaranya adalah sebagai berikut :Mengubahnya Menjadi Operasi Akar
Untuk mengubah bilangan pangkat pecahan menjadi akar, bisa menggunakan rumus :
am/n = aa1/n x m = (a1/n)m
Misalkan kita ingin menyelesaikan bilangan 272/3
Penyelesaian :
272/3 = 271/3 x 2 = (271/3)2 = (3√27)2 = 32 = 9
Mengubah Bilangan Pokok Menjadi Bilangan Berpangkat Sama Dengan Penyebut Pada Pangkat Pecahan
Dengan menggunakan cara ini kita bisa menyelesaikan soal bilangan berpangkat pecahan tanpa harus mengubahnya terlebih dahulu ke dalam bentuk operasi akar.
Perhatikan baik - baik contoh berikut ini :
43/2 = (22)3/2 = 22x3/2 = 23 = 8
272/3 = (33)2/3 = 33x2/3 = 32 = 9
Untuk memperluas pengetahuan kalian tentang materi ini, pelajari beberapa contoh soal dan pembahasan bilangan pangkat berikut ini :
Pecahan
Contoh Soal 1 :
a. 51/2
b. 63/2
c. 127/2
Penyelesaian :
a. 51/2 = √5
b. 63/2 = √63
c. 127/2 = √127
Contoh Soal 2 :
Sederhanakanlah bentuk - bentuk pecahan berikut ini :
a. 65/2 x 63/2
b. 31/2 x 31/2
c. (45/2)3/5
Penyelesaian :
a. 65/2 x 63/2 = 6(5/2) + (3/2) = 68/2 = 64 = 1296
b. 31/2 x 31/2 = 3(1/2) + (1/2) = 31 = 3
c. (45/2)3/5 = 4(5/2 x 3/5) = 415/10 = 43/2