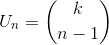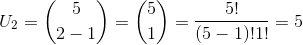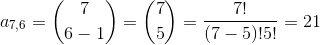Rangkuman Materi Operasi Pembagian Bilangan Bulat Dilengkapi Pembahasan Contoh Soal Lengkap

Operasi Pembagian Bilangan Bulat - Dalam artikel kali ini, admin akan menjelaskan materi mengenai operasi pembagian bilangan bulat. Sebelum kalian mempelajari materi ini terlebih dahulu kalian harus memahami konsep Operasi Perkalian Bilangan Bulat seperti yang telah disampaikan dalam materi sebelumnya. Karena bentuk operasi pembagian merupakan kebalikan dari operasi perkalian pada bilangan bulat. Untuk memahami materi mengenai operasi pembagian bilangan bulat, perhatikan pembahasan di bawah ini.

Pembagian Bilangan Bulat Positif dan Negatif

Hasil bagi antara bilangan bulat positif dengan bilangan bulat negatif adalah bilangan bulat negatif.
Contoh :
1. -5 x (-7) = 35, maka :
      35 : (-7) = -5
      35 : (-5) = -7
2. -4 x (-8) = 32, maka :
      32 : (-4) = -8
      32 : (-8) = -4
3. -11 x (-24) = 264, maka :
      264 : (-24) = -11
      264 : (-11) = -24
Di mana untuk setiap bilangan bulat a dan b selalu berlaku a : (-b) = -(a : b).

Pembagian Bilangan Bulat Negatif Dengan Bilangan Bulat Negatif

Hasil bagi antara bilangan bulat negatif dengan bilangan bulat negatif adalah bilangan bulat positif.

Contoh :

1. 5 x (-8) = -40, maka :

      -40 : (-8) = 5

2. -9 x 2 = -18, maka :

      -18 : (-9) = 2

3. 7 x (-4) = -28, maka :

      -28 : (-4) = 7

Di mana untuk setiap bilangan bulat a dan b selalu berlaku (-a) : (-b) = (a : b).

Pembagian Bilangan Bulat Dengan Nol (0)

Untuk mengetahui operasi pembagian bilangan bulat dengan nol (0), kita mengingat kembali perkalian bilangan bulat dengan nol (0). Di mana untuk setiap bilangan bulat a selalu berlaku a x 0 = 0 => 0 : a = 0.

Dari definisi di atas, dapat dituliskan bahwa "untuk setiap bilangan bulat a, berlaku 0 : a = 0 dan a ≠ 0". Hal tersebut tidak berlaku jika a = 0, karena 0 : 0 hasilnya tidak terdefinisi. Kesimpulannya adalah "jika bilangan nol (0) dibagi dengan bilangan bulat (bukan nol) maka hasilnya akan selalu nol (0).

Demikianlah pembahasan materi mengenai Operasi Pembagian Bilangan Bulat Dilengkapi Pembahasan Contoh Soal. Semoga kalian bisa memahami materi ini dengan mudah, sehingga bisa membantu kalian dalam mengerjakan soal - soal operasi pembagian bilangan bulat.

Rangkuman Materi Sifat - Sifat Operasi Hitungan Dilengkapi Pembahasan Contoh Soal Lengkap

Sifat - Sifat Operasi Hitungan - Pada artikel kali ini, admin akan membahas materi tentang sifat - sifat operasi hitungan. Selain kita bisa menghitung jumlah dan menyelesaikan suatu operasi hitungan, kita juga harus memahami sifat - sifat dalam pengoperasian hitungan misalkan, 20 + 12 = 32 akan sama hasilnya dengan 12 + 20 = 32 artinya kedua bilangan {(20 dan 12)} ditukarkan hasilnya tetap sama. Selain dari sifat tersebut masih ada sifat - sifat operasi hitungan yang lain. Untuk lebih jelasnya, perhatikan baik - baik penjelasan materi di bawah ini.

Sifat - Sifat Operasi Hitung Bilangan
1. Sifat Komutatif

Suatu bilangan penjumlahan atau perkalian jika kedua bilangan tersebut ditukarkan, maka hasilnya akan tetap sama. Artinya, sifat komutatif merupakan sifat pertukaran.
Contoh :
=> Penjumlahan : 7 + 8 = 15 dan 8 + 7 = 15 jadi, 7 + 8 = 8 + 7
=> Perkalian : 5 x 9 = 45 dan 9 x 5 = 45 jadi, 5 x 9 = 9 x 5
Sifat komutatif tidak berlaku pada pengurangan.
Contoh : 6 - 3 = 3 dan 3 - 6 = -3 (jika kedua bilangan ditukarkan hasilnya tidak sama).

2. Sifat Asosiatif

Suatu operasi penjumlahan atau perkalian tiga buah bilangan yang dikelompokkan secara berbeda, hasil operasinya akan tetap sama. Artinya, sifat asosiatif merupakan sifat pengelompokkan.
Contoh :
=> Penjumlahan : (3 + 4) + 8 = 7 + 8 = 15 dan 3 + (4 + 8) = 3 + 12 = 15
     Jadi, (3 + 4) + 8 = 3 + (4 + 8)
=> Perkalian : (8 x 2) x 5 = 16 x 5 = 80 dan 8 x (2 x 5) = 8 x 10 = 80
     Jadi, (8 x 2) x 5 = 8 x (2 x 5)

3. Sifat Distributif

Sifat distributif merupakan sifat penyebaran.

Contoh :
=> Penjumlahan : 3 x (7 + 9) = 3 x 16 = 48
                             (3 x 7) +  (3 x 9) = 21 + 27 = 48
     Jadi, 3 x (7 + 9) = (3 x 7) +  (3 x 9)
=> Pengurangan : 3 x (7 - 9) = 3 x (-2) = -6
                              (3 x 7) - (3 x 9) = 21 - 27 = -6
     Jadi, 3 x (7 - 9) = (3 x 7) - (3 x 9)

4. Menggunakan Sifat - Sifat Operasi Hitungan

Sifat disributif bisa digunakan pada perkalian dua bilangan, di mana salah satu bilangannya merupakan bilangan yang cukup besar. Perhatikan pembahasan contoh soal berikut ini.

Contoh 1 :

1. 2 x 156 = ....

2. 5 x 74 = ....

Penyelesaian :

1. 2 x 156 = 2 x (100 + 50 + 6)

                 = (2 x 100) + (2 x 50) + (2 x 6)

                 = 200 + 100 + 12

                 = 312

    Jadi, 2 x 156 = 312

2. 5 x 74 = 5 x (70 + 4)

               = (5 x 70) + (5 x 4)

               = 350 + 20

               = 370

   Jadi, 5 x 74 = 370

Conoh 2 :

1. (2 x 80) + (2 x 35) = ....

2. (5 x 40) + (5 x 74) = ....

Penyelesaian :

1. (2 x 80) + (2 x 35) = 2 x (80 + 35)

                                   = 2 x 115

                                   = 230

    Jadi, (2 x 80) + (2 x 35) = 230

2. (5 x 40) + (5 x 74) = 5 x (40 + 74)

                                   = 5 x 114

                                   = 570

    Jadi, (5 x 40) + (5 x 74) = 570

Demikianlah pembahasan materi mengenai Sifat - Sifat Operasi Hitungan Dilengkapi Dengan Pembahasan Contoh Soal. Semoga kalian bisa memahami penjelasan materi di atas sehingga artikel ini bisa membantu kalian dalam menyelesaikan soal - soal dalam bentuk operasi hitungan.

Rangkuman Materi Sifat - Sifat Perkalian Pada Bilangan Bulat Dilengkapi Pembahasan Contoh Soal Lengkap

Sifat - Sifat Perkalian Pada Bilangan Bulat - Artikel kali ini akan membahas tentang sifat - sifat perkalian bilangan bulat, dimana perkalian merupakan operasi penjumlahan dengan bilangan yang sama. Misalkan 6 x 3 = 3 + 3 + 3 + 3 + 3 + 3 = 18 sama halnya dengan 3 x 6 = 6 + 6 + 6 = 18. Meskipun hasil akhirnya sama, tetapi memiliki arti yang berbeda, di mana 6 x 3 artinya enam kali tiganya, sedangkan 3 x 6 artinya tiga kali enamnya. Pernyataan tersebut dapat dituliskan dengan n x a = a + a + a ... + a, artinya n merupakan banyaknya suku a. Penjelasan tersebut merupakan definisi perkalian pada bilangan bulat. Dalam perkalian bilangan bulat ada beberapa sifat perkalian yang perlu kalian pahami sebelum mengerjakan soal - soal. Untuk lebih memahami materi ini, perhatikan baik - baik penjelasan di bawah ini.

Sifat - Sifat Perkalian Bilangan Bulat
1. Hasil perkalian dua bilangan bulat dilihat dari tanda bilangannya

a. Hasil perkalian bilangan bulat positif akan selalu menghasilkan bilangan bulat positif.
Di mana setiap bilangan bulat a dan b selalu berlaku a x b = ab atau (+) x (+) = (+). Contoh : 5 x 8 = 40

b. Hasil perkalian bilangan bulat positif dengan bilangan bulat negatif adalah bilangan bulat negatif.
Di mana setiap bilangan bulat a dan b selalu berlaku a x (-b) = -ab atau (+) x (-) = (-). Contoh : 3 x (-7) = -21

c. Hasil perkalian bilangan bulat negatif dengan bilangan bulat positif adalah bilangan bulat negatif.
Di mana setiap bilangan bulat a dan b selalu berlaku -a x b = -ab atau (-) x (+) = (-). Contoh : -2 x 9 = -18

d. Hasil perkalian bilangan bulat negatif dengan bilangan bulat negatif adalah bilangan bulat positif.
Di mana setiap bilangan bulat a dan b selalu berlaku -a x -b = ab atau (-) x (-) = (+). Contoh : (-7) x (-5) = 35

2. Hasil perkalian antara bilangan bulat dengan nol (0) adalah nol (0)

Di mana setiap bilangan bulat a selalu berlaku a x 0 = 0 atau (0 x (a) = (0).
Contoh : 1. 5 x 0 = 0

                2. -7 x 0 = 0
                3. 0 x 3 = 0

3. Unsur Identitas Perkalian

Setiap bilangan bulat apabila dikalikan dengan 1, maka akan menghasilkan bilangan itu sendiri.
Contoh : 1. 9 x 1 = 0
                2. 25 x 1 = 25

                3. -18 x 1 = -18

Dalam hal ini, 1 disebut sebagai unsur identitas pada perkalian. Di mana untuk setiap bilangan bulat a selalu berlaku a x 1 = 1 x a = a.

4. Sifat Komutatif (pertukaran) perkalian

Setiap bilangan bulat a dan b selalu berlaku a x b atau b x a.
Contoh : 3 x 8 = 24 atau 8 x 3 = 24

5. Sifat Asosiatif (pengelompokkan) perkalian

Setiap bilangan bulat a, b, dan c selalu berlaku (a x b) x c => a x (b x c).
Contoh : (2 x 5) x 8 => 2 x (5 x 8)

6. Sifat distributif (penyebaran) perkalian

a. Sifat distributif perkalian terhadap penjumlahan

Setiap bilangan bulat a, b, dan c selalu berlaku a x (b + c) = (a x b) + (a x c).

Contoh : 2 x (8 + 7) = (2 x 8) + (2 x 7)

b. Sifat distributif perkalian terhadap pengurangan

Setiap bilangan bulat a, b, dan c selalu berlaku a x (b - c) = (a x b) - (a x c).

Contoh : 2 x (8 - 7) = (2 x 8) - (2 x 7)

7. Sifat tertutup pada perkalian

Setiap sembarang bilangan bulat a dan b, jika a x b = c, maka c juga merupakan bilangan bulat.

Contoh : 4 x 9 = 36

Di mana 4 dan 9 merupakan bilangan bulat dan 36 juga merupakan bilangan bulat.

Demikianlah pembahasan materi mengenai Sifat - Sifat Perkalian Pada Bilangan Bulat, semoga kalian bisa memahami penjelasan materi ini sehingga bisa membantu kalian dalam mengerjakan soal - soal tentang perkalian bilangan bulat. Untuk menambah wawasan kalian, pelajari juga materi tentang Operasi Perkalian Bilangan Bulat Dilengkapi Pembahasan Contoh Soal, semoga bermanfaat.

Rangkuman Materi Operasi Perkalian Bilangan Bulat Dilengkapi Pembahasan Contoh Soal Lengkap

Operasi Perkalian Bilangan Bulat - Perkalian merupakan operasi penjumlahan dengan bilangan yang sama. Pernyataan tersebut akan dijabarkan dengan penjelasan contoh di bawah ini,
6 x 3 = 3 + 3 + 3 + 3 + 3 + 3 = 18
sama halnya dengan :
3 x 6 = 6 + 6 + 6 = 18

Dari contoh tersebut kita melihat bahwa hasil akhirnya adalah sama tetapi memiliki arti yang berbeda, di mana 6 x 3 artinya enam kali tiganya, sedangkan 3 x 6 artinya tiga kali enamnya. Pernyataan tersebut dapat dituliskan dengan n x a = a + a + a ... + a, artinya n merupakan banyaknya suku a.

Perkalian Bilangan Bulat Positif dan Negatif

Hasil Perkalian antara bilangan bulat positif dengan bilangan bulat negatif adalah bilangan bulat negatif. Perhatikan contoh soal di bawah ini :

1. 5 x (-3) = -15

2. 8 x (-7) = -56

3. 4 x (-6) = -24

Di mana untuk setiap bilangan bulat a dan b selalu berlaku a x (-b) = -ab

Perkalian Bilangan Bulat Negatif dan Positif

Perkalian ini merupakan kebalikan dari perkalian positif dan negatif hanya berbeda pada bentuk soal sementara hasilnya sama yaitu bilangan bulat negatif. Perhatikan contoh berikut :

1. (-5) x 3 = -15

2. (-8) x 7 = -56

3. (-4) x 6 = -24

Di mana untuk setiap bilangan bulat a dan b selalu berlaku - (a x b) = -ab

Perkalian Bilangan Bulat Negatif Dengan Negatif

Hasil perkalian antara bilangan bulat negatif dengan bilangan bulat negatif adalah bilangan bulat positif. Perhatikan contoh berikut :

1. -4 x (-7) = 28

2. -6 x (-5) = 30

3. -3 x (-8) = 24

Di mana untuk setiap bilangan bulat a dan b selalu berlaku -a x (-b) => (a x b) = ab

Perkalian Bilangan Bulat Dengan Nol (0)

Untuk setiap bilangan yang dikalikan dengan nol (0), maka hasilnya adalah nol (0). Perhatikan contoh berikut :

1. 5 x 0 = 0

2. -7 x 0 = 0

3. 0 x 3 = 0

Unsur Identitas Perkalian

Setiap bilangan bulat apabila dikalikan dengan 1, maka akan menghasilkan bilangan itu sendiri. Perhatikan contoh berikut :

1. 9 x 1 = 0

2. 25 x 1 = 25

3. -18 x 1 = -18

Dalam hal ini, 1 disebut sebagai unsur identitas pada perkalian. Di mana untuk setiap bilangan bulat a selalu berlaku a x 1 = 1 x a = a.

Demikianlah pembahasan materi mengenai Operasi Perkalian Bilangan Bulat Dilengkapi Pembahasan Contoh Soal, semoga kalian bisa memahami penjelasan materi di atas dengan mudah sehingga artikel ini bisa membantu kalian dalam mengerjakan soal - soal perkalian bilangan bulat.

Rangkuman Materi Penyajian Data Menggunakan Tabel Distribusi Frekuensi Lengkap

Tabel Distribusi Frekuensi - Tabel distribusi frekuensi merupakan penyajian statistik data berkelompok dalam bentuk tabel, dimana setiap data dikelompokkan dalam kelas interval.
Dalam pembahasan materi kali ini, kita akan membahas bentuk penyajian tabel frekuensi, yaitu tabel frekuensi data tunggal dan tabel frekuensi data yang dikelompokkan. Untuk lebih jelasnya perhatikan penjelasan tabel frekuensi di bawah ini.

Tabel Frekuensi Data Tunggal

Penyajian data tunggal yang menggunakan tabel biasa disebut dengan istilah distribusi  frekuensi data tunggal. Berikut ini merupakan pembahasan contoh soal mengenai tabel distribusi data tunggal.

Diperoleh data jumlah anak yang dimiliki oleh 40 orang karyawan di PT. Karya Mandiri adalah sebagai berikut :

2  4  6  4  3  2  1  4  3  3
3  4  2  3  4  4  6  4  2  1
3  3  2  4  2  4  5  4  1  4
5  4  3  4  4  5  6  4  5  1

Dari data di atas, kita belum bisa mengetahui jumlah data yang sebenarnya karena data tersebut masih bersifat acak dan belum tersusun. Oleh sebab itu, kita harus menyajikannya ke dalam bentuk tabel frekuensi data tunggal agar kita bisa mengetahui informasi yang tersebut dengan benar.
Sebelum membuat tabel frekuensi data tunggal, kita harus memperhatikan terlebih dahulu langkah - langkah dalam membuat tabel, diantaranya pada kolom dan baris hanya memuat satu nilai atau data kemudian tabel dibagi menjadi tiga kolom. Kolom yang pertama diisi jumlah data. Pada kolom yang ke dua diisi dengan turus yaitu mencacah data dengan menggunakan lambang ( I ) sesuai dengan jumlah data yang diperoleh. Kemudian pada kolom terakhir diisi dengan frekuensi yang menyatakan jumlah turus pada setiap data.
Berikut adalah tabel dari data di atas :

Tabel Frekuensi Data Yang Dikelompokkan

Penyajian data berkelompok ke dalam bentuk tabel disebut dengan distribusi data berkelompok.

Untuk lebih memahami tabel distribusi berkelompok. Langsung saja perhatikan pembasan contoh soal berikut ini :

Diperoleh data nilai ulangan semester ganjil pelajaran matematika siswa kelas VIII SMP Teladan adalah bagai berikut :

64  67  89  90  82  70  91  73  52

75  64  73  83  70  52  57  57  49

89  79  82  50  59  52  82  65  53

96  54  99  92  74  44  73  91  85

Dari data di atas, kita sudah bisa mengetahui nilai yang tertinggi dan nilai terendah yang memiliki selisih atau jarak yang disebut dengan range (jangkauan). Dari data di atas jangkauannya cukup besar yaitu 99 - 44 = 55. Jika data di atas kita sajikan ke dalam bentuk data tunggal hasilnya tidak praktis dan tetap sulit untuk dipahami. Sehingga kita harus mengelompokkan data - data tersebut terlebih dahulu kemudian baru dimasukkan ke dalam tabel frekuensi berkelompok.

Dalam penyajian tabel frekuensi data berkelompok, ada beberapa langkah atau istilah yang sering digunakan. Berikut penjelasannya :

1. Kelas Interval

Mengelompokkan dari beberapa data atau nilai.

2. Banyak Kelas Interval

Banyaknya jumlah pengelompokkan dari keseluruhan data yang ada.

3. Panjang Interval

Banyaknya data di dalam satu kelas interval. Panjang interval di dalam suatu tabel haruslah sama.

Dari istilah - istilah di atas, kita bisa menggunakannya dalam menyajikan data tersebut ke dalam bentuk tabel frekuensi data berkelompok seperti berikut ini :

Tabel tersebut memiliki banyak kelas interval yaitu 7 dan panjang kelas intervalnya adalah 8.

Demikianlah penjelasan materi mengenai tata cara Penyajian Data Menggunakan Tabel Distribusi Frekuensi, semoga kalian bisa memahami penjelasan materi ini dengan mudah sehingga bisa membantu kalian dalam mengerjakan soal - soal yang menggunakan tabel distribusi frekuensi.

Rangkuman Materi Contoh Soal Dan Cara Penyelesaian Sistem Persamaan Linear Dua Variabel Melalui Metode Campuran Lengkap

Sistem Persamaan Linear Dua Variabel Melalui Metode Campuran - Sistem persamaan linear dua variabel menggunakan metode campuran merupakan cara penyelesaian sistem persamaan linear dua variabel yang menggabungkan metode eliminasi dan juga metode substitusi, dimana sistem persamaan linear dua variabel itu sendiri merupakan dua atau lebih persamaan linear dengan nilai variabel yang sama. Dan nilai sistem persamaan linear dua variabel metode substitusi adalah cara penyelesaian SPLDV dengan cara mengganti variabel dengan nilai sementara untuk mendapatkan nilai variabel yang sebenarnya. Sedangkan sistem persamaan linear dua variabel menggunakan metode eliminasi adalah menghilangkan salah satu dari suatu variabel sampai menyisakan satu variabel lainnya. Jadi cara penyelesaian sistem persamaan linear dua variabel dengan metode campuran ataupun kombinasi ini bisa dikatakan lebih mudah dan simple karena menggabungkan kedua cara tersebut. Dalam penyelesaiannya metode campuran akan terlebih dahulu menggunakan eliminasi dalam mencari salah satu nilai dari variabelnya, dan ketika nilai tersebut didapatkan maka hasil dari nilai variabel tersebut di substitusikan untuk mencari variabel yang lainnya.
Nah, diatas saya telah menjelaskan tentang definisi dari sistem persamaan linear dua variabel menggunakan metode campuran, maka untuk lebih jelasnya disini saya akan memberikan contoh soal beserta penyelesaian dari suatu sistem persamaan linear dua variabel dengan menggunakan metode campuran yang bisa dengan mudah untuk dipelajari.

Pembahasan Contoh Soal Metode Eliminasi Substitusi (Gabungan)

Contoh soal 1:
Tentukanlah himpunan dari sistem persamaan linear dua variabel  di bawah ini melalui metode campuran :
6x + 10y = 16
  x + 4y = 12

Penyelesaian :
Langkah pertama kita menggunakan metode eliminasi terlebih dahulu :
6x + 10y = 16
x + 4y = 12
Sehingga :
6x + 10y =16  |X1| → 6x + 10y = 16
x + 4y =12      |X6| → 6x + 24y = 72 -
                                             -14y = -56
                                                  Y = 4
Jadi, nilai dari y adalah 4, setelah itu baru kita substitusikan ke bentuk persamaan yang ke dua :
x + 4y = 12
x + 4 (4) = 12
x + 16 = 12
x = 12 - 16
x = -4
Jadi, hasil himpunan dari 6x + 10y = 16 dan x + 4y = 12 adalah {(4, -4)}

Contoh soal 2 :
Rio membeli 4 buah penggaris dan 2 buah penghapus di sebuh toko alat tulis dengan harga Rp. 10.000,-. Jika Rio kembali membeli 3 buah penghapus dan 8 buah penggaris di toko yang sama dengan harga Rp. 19000,-. Maka berapakah harga dari 2 buah penggaris dan dua buah penghapus jika Rio membeli kembali di toko tersebut ?

Penyelesaian :
Yang kita lakukan pertama adalah melambangkan bahwa penggaris ditulis dengan lambang x dan penghapus dengan lambang y, maka persamaannya adalah :
4x + 2y = 10.000…(1)
8x + 3y = 19.000…(2)
Sehingga :
4x + 2y = 10.000 |x8| → 32x + 16y = 80.000
8x + 3y = 19.000 |x4| → 32x + 12y = 76.000 -
                                                       4y  = 4000
                                                          Y = 1000
Nah, setelah nilai dari y kita temukan sekarang kita bisa mencari nilai dari x melalui metode substitusi, yaitu :
32x + 16 y = 80.000
32x + 16 (1000) = 80.000
32x + 16000 = 80.000
32x = 80.000 – 16000
32x = 64000
    X = 2000
Jadi, harga dari x adalah 2000

Karena nilai dari x dan y sudah di ketahui maka kita bisa mensubstitusikannya kembali untuk memperoleh jumlah harga dari 2 buah penggaris dan juga dua buah penghapus dengan 2x + 2y…???
2x + 2y = …
2 (2000) + 2 (1000) = …
4000 + 2000 = 6000
Jadi, bisa disimpulkan bahwa harga dari dua buah penggaris dan juga dua buah penghapus adalah Rp. 6000,-

Demikianlah penjelasan materi mengenai penyelesaian Sistem Persamaan Linear Dua Variabel Menggunakan Metode Campuran yang bisa kita aplikasikan dalam penyelesaian soal-soal berikutnya yang berhubungan dengan SPLDV metode campuran. Semoga bermanfaat.

Rangkuman Materi Cara Menyelesaikan Soal Sistem Persamaan Linear Dua Variabel Dengan Metode Eliminasi Lengkap

 Pada Artikel sebelumnnya, Belajar Matematikaku sudah menjelaskan materi yang berkaitan dengan SPLDV yaitu tentang Sistem Persamaan Linear Dua Variabel Dengan Metode Substitusi. Sistem persamaan linear dua variabel merupakan suatu kesatuan dari persamaan linear dua variabel yang sejenis. Dalam penyelesaian sistem persamaan linear dua variabel kita bisa menggunakan metode substitusi, metode grafik, metode  eliminasi dan juga metode eliminasi substitusi. Dalam penjelasan kali ini kita akan membahas bagaimana penyelesaian sistem persamaan linear dua variabel menggunakan metode eliminasi. Untuk lebih jelasnya, perhatikan baik - baik penjelasan dan contoh soal di bawah ini.

Sistem Persamaan Linear Dua Variabel Dengan Metode Eliminasi

Penggunaan metode eliminasi dalam sistem persamaan linear dua variabel yaitu dengan terlebih dahulu mengeliminasi atau menghilangkan salah satu dari variabel, baik menggunakan penjumlahan maupun pengurangan. Yang perlu diperhatikan dari pengeliminasian suatu variabel ini kita harus  terlebih dahulu memperhatikan koefisien dari variabel tersebut, jika koefisien dari  variabelnya belum sama kita harus terlebih dahulu menyamakan koefisien tersebtu baik dengan cara membagi maupun mengalikannya, setelah langkah tersebut barulah kita bisa menentukan variabel yang lainnya. Karena daalam metode eliminasi kita perlu mengeliminasi dua kali variabel tersebut.  Koefisien dari variabel itu sendiri  adalah suatu bilangan yang menyatakan seberapa banyaknya jumlah suatu variabel yang sejenis atau bisa juga di katakan sebagai bilangan yang berada paling depan variabel. Variabel biasanya di lambangkan menggunakan huruf  “x” dan juga “y”. Jadi untuk metode eliminasi kita perlu menghilangkan salah satu dari variabel tersebut, misalkan mencari variabel “x” maka kita harus mengeliminasi variabel “y” begitu juga sebaliknya. Untuk lebih memahami tentang sistem persamaan linear dua variabel menggunakan metode eliminasi maka perhatikan contoh soal dan pembahasannya berikut ini.

Contoh soal :
Tentukan himpunan di bawah ini dengan penyelesaian sistem persamaan linear dua variabel menggunakan metode eliminasi dengan variabel x dan y pada himpunan bilangan real di bawah ini :
a. X + y = 4 dan x + 4 y = 4
b. 7x + 2y = 14 dan x - 2y = 10
c. 3x + 4y = 8 dan 6x - 4y = 6

Penyelesaian :
a. Untuk mencari x + y = 4 dan x + 4 y = 4 kita bisa menggunakan dua tahapan
Yang pertama kita harus mengeliminasi variabel y terlebih dahulu dengan catatan koefisien dari y harus sama yaitu x + y = 1 dikalikan 4 dan x + 4y = 4 dikalikan 1, jadi :
X + y = 1 | x4  | ↔ 4x + 4y = 4
X + 4y = 4 | x1 | ↔ x + 4y = 4
4x + 4y = 4
  x + 4y = 4 -
3x + 0   = 0
X = 0

Setelah itu kita eleminasi variabel x, pada langkah kedua kita tidak perlu lagi menyamakan koefisien untuk menghilangkan variabel x karena koefisiennya sudah sama, sehingga :
X + y = 1
X + 4y = 4 -
0 + -3y = -3
Y = 1
Jadi, himpunannya adalah {(0,1)}

b. 7x + 2y = 14 dan x - 2y = 10
Karena koefisien dari y sama maka kita bisa langsung memastikan bahwa koefisien y yang harus dihilangkan dengan cara menjumlahkannya, maka :
7x + 2y = 14
x – 2y   = 10 +
8x         = 24
  X = 3

7x + 2y =14 | x1 | ↔ 7x + 2y = 14
 x – 2y = 10 | x7 | ↔ 7x – 14y = 70 -
                                            16y = -56
                                                Y = -3,5
Jadi himpunannya adalah {(3 dan -3,5)}

c. 3x + 4y = 8 dan 6x - 4y = 6
Soal c sama dengan pembahasan di soal b karena koefisien y sama jadi kita bisa langsung mengeliminasi koefisien y, sehingga :
3x + 4y = 8
6x - 4y = 6 +
9x        = 14
  X = 1,5

3x + 4y = 8 | x6 | 18x + 24y = 48
6x - 4y = 6 | x3 |  18x – 12y = 18 -
                                         36y = 30
                                             Y = 0,8
Jadi himpunannya adalah {(1,5 dan 0,8)}

Itulah tadi pembahasan mengenai Sistem Persamaan Linear Dua Variabel Dengan Metode Eliminasi, yang bisa di gunakan sebagai acuan bagi kita dalam mengerjakan soal – soal selanjut nya yang sering kita temui dalam pelajaran matematika, sehingga kita bisa dengan mudah menyelesaikannya. Semoga bermanfaat.

Rangkuman Materi Cara Menyelesaikan Soal Sistem Persamaan Linear Dua Variabel Dengan Metode Substitusi Lengkap

Sistem Persamaan Linear Dua Variabel Dengan Metode Substitusi - Sistem persamaan linear dua variabel adalah sistem persamaan linear yang terdiri dari dua variabel. Dalam menentukan suatu sistem persamaan linear dua variabel (SPLDV), ada beberapa metode penyelesaian yaitu dengan metode grafik, eliminasi, substitusi, dan eliminasi substitusi. Pada artikel kali ini, admin akan menjelaskan sistem persamaan linear dua variabel (SPLDV) dengan menggunakan metode substitusi.

Metode Substitusi

Substitusi dapat diartikan sebagai "mengganti" yaitu dengan menggabungkan antar variabel yang satu dengan yang lainnya yang hasilnya kemudian disubtitusikan kembali ke variabel selanjutnya untuk memperoleh hasil yang lainnya. Sebenarnya penyelesaian sistem persamaan linear menggunakan metode subtitusi tidaklah sulit kita hanya perlu menggabungkan variabel - variabel tersebut.
Untuk lebih jelasnya, perhatikanlah dengan seksama pembahasan contoh soal berikut ini.

Contoh 1 :
Carilah nilai dari x dan y dari sistem persamaan berikut ini melalui metode subtitusi.
6x + 2y = 20
X + y = 10

Pembahasan :
Yang pertama kita harus memasukkan terlebih dahulu persamaan yang satu dengan lainnya, karena persamaan yang kedua lebih simple, maka kita bisa mengubahnya menjadi 10 – x = y. Setelah diubah barulah kita masukkan ke persamaan yang pertama, maka :
6x + 2y = 20
6x + 2(10 - x) = 20
6x + 20 – 2x = 20
6x - 2x = 20 - 20
X = 0

Nah karena nilai dari x sudah diketahui maka kita bisa memasukkannya ke persamaan yang kedua untuk mencari nilai dari y, sehingga :
X + y = 10
0 + y = 10
Y = 10 + 0
Maka y = 10
Jadi, nilai dari x dan y adalah (0 dan 10)

Contoh 2 :
Temukan himpunan penyelesaian dari persamaan linear di bawah ini dengan menggunakan metode subtitusi.
3x + 5y = 13…pers…1
X + 9y = 17…pers…2

Penyelesaian :
Karena persamaan kedua lebih sederhana maka kita bisa menggunakannya untuk disubstitusikan ke persamaan yang pertama, namun terlebih dahulu harus diubah menjadi : x = 17 - 9y, maka :
3x + 5y = 13
3 (17 - 9y) + 5y = 13
51 – 27y + 5y = 13
-27 + 5y = 13 – 51
-22y = -38
Y = (1,7)

Karena nilai y sudah di ketahui, maka kita bisa langsung mensubtitusikannya ke persamaan x = 17 – 9y, untuk mencari nilai dari x, sehingga :
X = 17 – 9y
X = 17 – 9(1,7)
X = 17 – 15,3
X = 1,7
Jadi, himpunan penyelesaian dari  3x + 5y = 13…pers…1 dan X + 9y = 17…pers…2 adalah {1,7 dan 1,7}

Contoh 3 :
Gunakan metode substitusi untuk menentukan himpunan dari sistem persamaan :
3x + 3y = …9 (1)
X + 6y = …13 (2)

Penyelesaian :
Untuk soal nomor tiga cara penyelesaiannya sama dengan nomor dua yaitu dengan
Mengekuivalenkan terlebih dahulu persamaan yang lebih sederhana yang kemudian dimasukkan persamaan yang satunya, maka :
3x + 3y = 9
3(13-6y) + 3y = 9
39 – 18y + 3y = 9
-18 + 3y = 9-39
-15 = 30
Y= 2
Jadi, y adalah 2
Setelah ini kita masukkan ke persamaan x = 13 – 6y
X = 13 – 6y
X = 13 – 6(2)
X = 13 – 12
X= 1
Jadi, hasil himpunannya adalah {2 dan 1}

Itulah ulasan mengenai Sistem Persamaan Linear Dua Variabel Menggunakan Metode Substitusi yang dimana menggunakan metode ini kita hanya perlu memasukkan salah satu dari persamaannya ke persamaan yang lain dengan mengekuivalenkannya terlebih dahulu untuk menghasilkan nilai yang lainnya, semoga dengan adanya artikel tentang sistem persamaan linear dua variabel ini bisa membantu kalian dalam mencari SPLDV dengan metode subtitusi.

Rangkuman Materi Pembahasan Dan Contoh Soal Penyelesaian Peluang Suatu Kejadian Lengkap

Peluang Suatu Kejadian - Peluang suatu kejadian merupakan besarnya nilai kemungkinan suatu kejadian yang akan muncul yang berasal dari perbandingan banyaknya titik sampel suatu kejadian yang di ambil dengan banyaknya anggota ruang sampel tersebut, atau peluang juga bisa dikatakan dengan nilai kemungkinan titik sampel dari suatu kejadian (bagian atau anggota yang berada dalam ruang sampel itu sendiri). Sedangkan ruang dari sampel tersebut merupakan kumpulan dari semua peristiwa maupun kejadian yang bisa saja muncul dari sebuah percobaan.

Jadi, peluang suatu kejadian bisa juga dikatakan sebagai suatu cara yang bisa kita gunakan untuk mengetahui seberapa besar kemungkinan suatu kejadian yang di harapkan akan muncul, dan frekuensi harapan adalah perbandingan dari banyak suatu percobaan yang di lakukan dengan banyaknya kejadian yang diamati. Untuk mencari frekuensi itu sendiri bisa kita ketahui melalui pembagian antara banyak kejadian dengan banyak percobaan yang dilakukan, dan jika tiap-tiap titik sampel anggota ruang s punya peluang yang sama maka jumlah kejadian (k) dengan jumlah anggota digambarkan menjadi  n(k) bisa diketahui melalui rumus :

 dengan k ⪽c.

Peluang suatu kejadian bisa kita ambil contoh melalui percobaan pelemparan koin maupun pelemparan dadu. Sedangkan nilai dari peluang kejadian memiliki sifat 0 p 1, maksudnya jika p = 0 maka kejadian itu tidak mungkin terjadi, atau mustahil. Namun jika p = 1 maka kejadiannya bisa dipastikan terjadi.
Untuk lebih jelasnya disini saya akan memberikan penjelasan mengenai soal suatu peluang kejadian dan pembahasannya berikut ini.

Contoh 1:
Ketika sebuah dadu dilemparkan ke udara  maka carilah peluang munculnya dadu dengan angka genap, dan juga dadu berangka 9 ?

Jawab:
Ruang sampel = 1, 2, 3, 4, 5, dan 6
Berarti n(s) = 6
Mata dadu genap = (2, 4, dan 6)
N(s) = 3
Jadi, p(k) = 3/6 = ½ .
Untuk dadu berangka 9 mustahil muncul karena peluang dadu angka 9 tersebut mustahil terjadi dikarenakan dadu hanya memiliki 6 buah sisi.

Contoh 2 :
Di dalam sebuah kantong plastik terdapat 6 buah kelereng yang terdiri dari 1 buah kelereng yang berwarna biru, 2 buah kelereng berwarna hijau, dan juga 3 buah kelereng dengan warna hitam.
Jika kelereng tersebut diambil 3 kelereng dengan cara di acak namun kelereng tersebut harus di kembalikan lagi ke dalam kantong plastik. Maka seberapa besar peluang terambilnya kelereng secara berturut-turut berwarna biru, hijau, dan juga hitam ?

Jawab:
Karena kelereng yang telah di ambil harus di kembalikan lagi ke dalam kantong plastik maka kita bisa dengan mudah mengetahuinya karena nilai untuk setiap pengambilan kelereng tersebut masih tetap sama, yaitu : 1 + 2 + 3 yang berjumlah enam buah kelereng, sehingga besarnya peluang terambilnya kelereng dengan urutan warna biru, hijau, dan juga hitam adalah dengan perkalian dari tiga peluang terambilnya kelereng dengan setiap pengambilan, maka :

P = 6/6
Jadi, hasil peluang kejadian pengambilan kelereng tersebut adalah 6/6

Itulah langkah-langkah yang bisa kita jadikan sebagai landasan untuk menyelesaikan persoalan-persoalan yang bersangkutan dengan Peluang Kejadian Suatu Peristiwa, sehingga kita bisa mengetahui peluang terjadinya suatu peristiwa yang akan muncul seperti permainan dadu, melempar koin dan lain sebagainya. Semoga artikel ini bisa memberikan manfaat bagi kita semua.

Rangkuman Materi Cara Membuat Diagram Histogram Dan Poligon Frekuensi Lengkap

Diagram Histogram Dan Poligon Frekuensi - Histogram dan poligon merupakan dua grafik yang digunakan untuk menggambarkan distribusi frekuensi. Untuk lebih jelasnya, mari simak penjelasan materi di bawah ini.

Pengertian Histogram dan Poligon Frekuensi

Histogram merupakan data yang telah disusun dalam bentuk tabel distribusi frekuensi yang disajikan dalam bentuk diagram kotak yang lebarnya menunjukkan interval kelas, sedangkan batas - batas tepi kotak merupakan tepi bawah dan tepi atas kelas dan tingginya menunjukkan frekuensi kelas tersebut.
Poligon frekuensi merupakan titik - titik tengah sisi atas dari histogram yang dihubungkan satu sama lain oleh ruas - ruas garis.
Untuk lebih jelasnya perhatikan contoh soal di bawah ini :
Diketahui data nilai Ujian Tengah Semester Matematika kelas VI SD Mandiri dari 50 siswa digambarkan dalam bentuk tabel sebagai berikut :

Dari tabel di atas, data dikelompokkan menjadi tujuh interval. Interval yang pertama yaitu 50 - 54 dan frekuensinya adalah 2, artinya siswa yang mendapatkan nilai 50 - 54 sebanyak 2 siswa. Pada interval tersebut, nilai 50 menjadi batas bawah dan nilai 54 menjadi batas atas kelas.

Selain batas atas dan batas bawah, dikenal juga istilah tepi bawah dan tepi atas yang berfungsi sebagai penentu panjang dari kelas interval jika data - data telah disajikan dalam bentuk tabel distribusi frekuensi.

Berikut cara menentukan tepi atas dan tepi bawah :

Tepi atas = batas atas + 0,5

Tepi bawah = batas bawah - 0,5

Sedangkan selisih dari tepi atas dan tepi bawah merupakan panjang interval. Kita ambil contoh dari interval yang pertama, yaitu 50 - 54 dengan cara di bawah ini :

Tepi atas = 54 + 0,5 = 54,5

Tepi bawah = 50 - 0,5 = 49,5

Panjang interval = 54,5 - 49,5 = 5

Histogram

Dari penjelasan tabel di atas bisa dibentuk sebuah diagram yang disebut sebagai histogram. Histogram batang hampir sama dengan diagram batang hanya pada histogram bentuk batang - batang yang ada saling berhimpitan dan disetiap batang menentukan kelas tertentu yaitu lebar pada batang menunjukkan panjang kelas sementara tinggi batang menunjukkan frekuensinya.

Berikut ini gambar histogram dari penjelasan tabel di atas :

 Poligon Frekuensi

Selain digambarkan dengan histogram, penjelasan dari data di atas bisa juga digambarkan dengan menggunakan Poligon Frekuensi yaitu dengan menghubungkan titik - titik tengah dari setiap interval secara berurutan. Supaya ujung - ujung poligon frekuensi terlihat tertutup, maka sebelum kelas paling bawah dan setelah kelas paling atas kita tambahkan satu kelas dengan frekuensi nol (0).

Untuk lebih jelasnya perhatikan gambar poligon frekuensi di bawah ini :

Demikianlah penjelasan materi mengenai Diagram Histogram Dan Poligon Frekuensi, Semoga kalian bisa memahami materi ini dengan mudah sehingga bisa membantu kalian dalam menyelesaikan soal - soal.

Kunci Jawaban Ujian Sekolah (US/UN) Matematika Kelas 6 SD/MI 17 Mei 2016 Utama

Kunci Jawaban Soal Ujian Sekolah/Ujian Nasional (US/UN) Asli Utama SD-MI Tujuh Belas Mei 2016 Matematika paket 2 ( kode P2 ) Jawa Tengah yang sudah diujikan pada tanggal 17 Mei 2016 _Siswa kelas 6 Sekolah Dasar/Madrasah sudah mulai lega. pasalnya mereka sudah mengerjakan soal Ujian Sekolah Mata Pelajaran Matematika tahun pelajaran 2015/2016. Selain para siswa, para guru dan orang tua/wali siswa kelas 6 SD/MI juga ikut merasa lega walaupun pengumuman nilai hasil ujian sekolah baru bisa didapatkan secara resmi pada bulan Juni 2016. Mereka sudah cukup lega karena mayoritas siswa peserta US/UN SD 2016 disuruh menyalin hasil jawaban sebelum lembar jawaban ujian dikumpulkan ke pengawas/panitia ujian. Setelah US selesai, para guru (khususnya guru kelas 6)  mayoritas langsung membuat kunci jawaban us/un sebagai dasar untuk mencocokkan hasil pekerjaan siswa, yang selanjutnya guru mengoreksi lembar jawab salinan tersebut.

Dengan demikian, paling tidak para guru dan siswa serta orang tua/wali murid sudah memiliki gambaran dan/atau mengetahui tentang nilai yang diperoleh oleh siswa kelas 6 SD/MI dan seperti pengalaman tahun-tahun sebelumnya, biasanya nilai prediksi US dengan nilai resmi tidak meleset, misalnya ada yang meleset ya paling selisih sedikit.

Kunci Jawaban US/UN SD-MI Matematika 17 Mei 2016 Paket 2 Jateng:

1. C
2. D
3. B
4. D
5. C
6. B
7. A
8. C
9. B
10. C
11. D
12. A
13. A
14. D
15. D
16. A
17. A
18. B
19. C
20. D
21. B
22. C
23. B
24. C
25. C
26. C
27. B
28. B
29. D
30. A
31. C
32. D
33. D
34. A
35. C
36. D
37. C
38. A
39. C
40. D

Demikian tentang Kunci Jawaban Ujian Sekolah (US) atau Ujian Nasional (UN) Mata Pelajaran Matematika Kelas 6 SD/MI 2016 Utama. Semoga arsip kunci jawaban US SD 2016 Matematika ini juga bisa bermanfaat bagi siswa kelas 6 SD/MI 2016-2017-2018. baca juga Cara Mudah Menentukan Kelipatan Bilangan Bulat Positif

Rangkuman Materi Memahami Rumus Segitiga Pascal dalam Matematika Lengkap

Rumus Segitiga Pascal dalam Matematika -  Segitiga pascal merupakan sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga. Manfaat dari segitiga pascal ini salah satunya yaitu untuk menyelesaikan soal perpangkatan dengan cepat, dari segitiga pascal ini kita tidak perlu mengalikan bilangan satu persatu tetapi bisa langsung mengetahui koefisien dari penyelesaian soal perpangkatan.
Perhatikan gambar segitiga pascal berikut ini :

Lima barisan pertama pada segitiga pascal

Dari gambar segitiga pascal di atas, bisa kita lihat bahwa puncak bagian teratas baris ke - 0 diisi dengan angka 1. Kemudian di bawahnya (baris ke - 1) diisi dengan angka 1 dan 1. Kemudian baris selanjutnya (baris ke - 2) masih diisi dengan angka 1 dan 1 dibagian sisinya kemudian pada bagian dalam diisi dengan hasil dari penjumlahan dua bilangan yang ada di atasnya yaitu 1+1=2.

Untuk baris ke - 3 diisi dengan angka 1 dan 1 pada bagian sisi kemudian bagian tengahnya diisi dengan hasil dari penjumlahan dua bilangan yang ada pada baris ke - 2 yaitu 1+2=3. Kemudian baris keempat (angka 4) dihasilkan dari penjumlahan dua bilangan yang ada di atasnya, yaitu 1+3=4 begitu juga angka 6 dihasilkan dari penjumlahan dua bilangan yang ada di atasnya yaitu 3+3=6, dan seterusnya.

Rumus Segitiga Pascal

Penyederhanaan bentuk  merupakan koefisien dari setiap baris segitiga pascal, yang apabila dijabarkan maka akan terlihat bahwa koefisien yang diperoleh dari bentuk tersebut sama persis dengan bilangan yang ada pada setiap baris segitiga pascal di atas.
Untuk lebih jelasnya perhatikan bentuk penyederhanaan berikut :

1.  (a + b)¹ = a + b → Koefisiennya adalah 1 dan 1
2. (a + b)² = a² + 2ab + b² → Koefisiennya adalah 1, 2, dan 1 
3. (a + b)³ = (a + b) (a² +2ab + b²⁾
                   = a³ + 2a²b + ab² + a²b + 2ab² + b³
                   = a³ + 3a²b + 3ab² + b³ → Koefisiennya adalah 1, 3, 3, dan 1

Semua bilangan di atas merupakan koefisien dari expansi pangkat binomial,
Perhatikan contoh berikut :

(x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

dari contoh tersebut, pada i = 4 diperoleh koefisien dari expansi pangkat binomial 4 yaitu 1, 4, 6, 4, dan 1 yang merupakan bilangan - bilangan yang mengisi baris ke - 4 pada segitiga pascal.
Perhatikan teorema binomial berikut :

               

Dari uraian di atas, secara umum bisa disimpulkan bahwa barisan bilangan pada baris i = k dalam segitiga pascal dapat dituliskan menjadi :

 

Lebih jelasnya, kita ambil contoh dari bilangan ke - 2 dan ke - 3 pada baris ke - 5 dalam segitiga pascal, sehingga :

Berdasarkan pola di atas diperoleh rumus baru yang bisa digunakan untuk menentukan bilangan a_i,j yang merupakan bilangan pada baris ke - i dan kolom ke - j, seperti di bawah ini :

Kemudian, misalkan kita akan mencari bilangan baris ke - 7 tepat pada kolom ke - 6, maka rumusnya :

Dari penjabaran rumus di atas, barisan bilangan ke - d dapa dituliskan sebagai berikut :

Sebagai pembuktian dari rumus di atas, kita coba mencari diagonal ke - 3 yang memiliki pola n(n + 1) / 2 dalam segitiga pascal dengan d = 3, sehingga :

Demikianlah penjelasan materi tentang Rumus Segitiga Pascal dalam Matematika, semoga kalian bisa memahami materi ini dengan mudah sehingga bisa membantu kalian dalam mengerjakan soal - soal. Selamat belajar.

Rangkuman Materi Sifat - sifat Barisan Atau Deret Aritmetika Dilengkapi Pembahasan Contoh Soal Lengkap

Sifat - Sifat Barisan - Barisan bilangan merupakan susunan bilangan-bilangan yang memiliki pola atau aturan tertentu antara satu bilangan dengan bilangan berikutnya, sedangkan bilangan - bilangan yang membentuk suatu barisan biasa disebut dengan suku-suku barisan. Bilangan pertama atau suku pertama dalam barisan tersebut  biasa dilambangkan dengan huruf U1, suku kedua U2, suku ketiga U3, dan seterusnya. Sampai suku ke-n dengan Un (n adalah bilangan asli).
Indeks n menyatakan suku dalam barisan suku ke-n yang di lambangkan dengan Un disebut "suku umum barisan". Pada umumnya suku ke-n atau Un merupakan fungsi dengan daerah asal (domain) bilangan asli n.

Contoh barisan bilangan:
1, 2, 3, 4, 5, 6, …………Un.
Rumus umum yang bisa di gunakan untuk mencari suku ke-n atau Un dapat di tentukan dengan cara mengamati pola atau aturan tertentu yang terdapat pada tiga atau empat suku pertama dari barisan tersebut.

Barisan Aritmetika
Barisan aritmetika merupakan barisan yang memiliki ciri-ciri tertentu, yaitu selisih antara dua suku yang berurutan mempunyai nilai yang tetap (konstan), sedangkan selisih dari dua suku yang berurutan disebut sebagai beda dari barisan aritmetika yang biasa dilambangkan dengan huruf b.

Contoh :
1). Untuk barisan 1, 4, 7, 10,… beda (b) = 10 – 7 = 7 – 4 = 4 – 1 = 3
2). Untuk barisan 6, 4, 2, 0,... beda (b) = 0 – 2 = 2 – 4 = 4 – 6 = -2
Kita hanya perlu mengurangkan antar suku tersebut untuk mengetahui beda dari barisan tersebut.
Sedangkan deret merupakan suku-suku beruntun dari suku-suku suatu barisan, misalkan 1, 3, 5, 7, melalui hubungan sebagai berikut :
Misalkan suatu barisan aritmetika dengan suku pertama a  dan beda b, maka rumus umumnya bisa di tentukan oleh : Un = a + (n – 1) b

Deret juga merupakan jumlah suku - suku suatu barisan yang biasa di sebut dengan penjumlahan beruntun. Misalkan U1, U2, U3,…,Un merupakan suku - suku suatu barisan yang biasa di tuliskan sebagai U1 +  U2 + U3+ …+ Un.
Dalam bentuk penjumlahan beruntun tersebut Un bisa disebut sebagai suku penjumlahan ke - n. Jika n merupakan  bilangan asli berhingga maka deret tersebut dinamakan deret berhingga. Untuk cara penulisan deret yang praktis kita bisa menuliskan tiga buah suku penjumlahan pertama yang  kemudian diikuti dengan tiga buah titik (…), dan diakhiri dengan suku penjumlahan yang terakhir.
Untuk lebih jelas dalam menghitung barisan dan deret aritmetika perhatikan pembahasan contoh soal berikut ini :

Contoh Soal Barisan Aritmetika :
a. Carilah suku pertama, beda, dan suku ke-5 dari barisan aritmetika 1, 3, 5, 7,…
b. Jika suku pertama dari barisan aritmetika sama dengan 4 dan bedanya adalah 7. Maka carilah suku ke - 10 dan suku ke berapa yang nilainya adalah 100?

Pembahasan :
Cara penyelesaiannya,
a.  Misalkan, a merupakan suku pertama, dan b (beda)
Barisan 1, 3, 5, 7.
Suku pertama   U1 = a = 1, beda "b" (untuk mencari beda kita hanya perlu mengurangkan suku kedua dengan ke satu) = 3 – 1 = 2
Suku ke 5 => U5 = a + 4b
U5 = 1 + 4(2)
U5 = 1 + 8
U5 = 9
Jadi, bisa diketahui  bahwa suku pertamanya 1, beda (b) = 2 dan juga suku kelimanya adalah 9.

b. Yang pertama kita harus mencari suku ke - 10 terlebih dahulu dengan menggunakan rumus :
Un = a + (n -1 ) b
Un = bn + (a - b)
a = 4
b = 7
Sehingga, Un = 4 + (n – 1) 7 = 7n – 5
Suku ke - 10 yaitu U10 = 7(10) – 5
                                       = 65
Jadi, suku ke - 10 nya adalah 65.
Setelah kita mengetahui suku ke - 10 barulah kita mencari suku ke berapa yang nilainya 100.
Un = 7n – 5
7n – 5 = 100
       7n = 105
         n = 105
                 7
         n = 15
Jadi, suku yang bernilai 100 adalah suku yang ke - 15.

Contoh Soal Deret Aritmetika :
a. Hitunglah jumlah 60 suku pertama dari deret - deret aritmetika 2 + 4  + 6 + 8 …
b. Hitunglah jumlah deret aritmetika berikut : 3 + 6 + 9 + … + 90
c. Diketahui suatu deret aritmetika adalah 2 + 6 + 10 + 14 + …. Maka tentukanlah rumus umum suku ke - n, rumus jumlah n suku pertamanya, dan juga hitunglah jumlah 60 suku pertamanya.

Penyelesaian :

a. Untuk mengetahui 60 suku pertama kita bisa menggunakan hubungan :

Sehingga,

         

Dari deret aritmetika 2 + 4 + 6 + 8… dapat diperoleh a = 2 dan b = 2
U60 = a + 58b = 2 + 58(2) = 118
S40  = 30 (a + U40) = 30 (2 + 118) = 3600.
Jadi, jumlah 40 suku pertama deret aritmetika tersebut adalah  S40 = 3600.

b. Untuk menyelesaikan jumlah deret aritmetika dari 3 + 6 + 9…+ 90
Kita bisa menggunakan hubungan Un = a + (n – 1) b
3 + 6 + 9 + …+ 90
a = 3, b = 3, dan un = 90
90 = 3 + (n – 1) 3 ↔ 90 = 3n ↔ n = 30

         = 15 (3 + 90) = 1395

Jadi, jumlah deretnya adalah S30 = 1395.

c. Baris arimetika dari deret adalah 2, 6, 10, 14… yang suku pertamanya a = 2 dan b = 4
Yang pertama kita harus mencari rumus umum suku ke - n.
Dengan rumus umum suku ke - n : Un = a + (n – 1) b
Un = 2 + (n – 1) 4
Un = 4n – 1
Jadi , rumus umumnya adalah Un = 4n – 1.
Untuk mencari jumlah n suku pertama kita gunakan rumus :

Jadi rumus umumnya adalah : 

Setelah itu barulah kita mencari 60 suku pertama :

Itulah penjelasan mengenai  Barisan Atau Deret Aritmetika Dilengkapi Pembahasan Contoh Soal yang bisa kita gunakan untuk menjumlahkan dan menentukan rumus dari baris dan deret aritmetika itu sendiri semoga bermanfaat.

baca juga :

• Rumus dan Pola Barisan Aritmatika
• Barisan dan Deret Aritmatika Matematika SMP Kelas 9 
• Materi Matematika Perbandingan Bertingkat

Rangkuman Materi Operasi Aljabar Pada Bentuk Akar Dilengkapi Pembahasan Contoh Soal Lengkap

Operasi Aljabar Pada Bentuk Akar - Operasi aljabar pada bentuk akar merupakan operasi dalam bentuk penjumlahan, pengurangan ,perkalian maupun pembagian dalam bentuk akar yang digunakan untuk menyederhanakan bentuk akar.

Penjumlahan dan Pengurangan Bentuk Akar

Sifat - sifat dari penjumlahan dan pengurangan bentuk akar yang biasa di gunakan secara umum bisa digambarkan berikut ini :

                                            a√b  + c√b  = (a + c) √b

                                            a√b  - c√b  = (a - c) √b

                                            dengan a, b, c, ∈R dan b ≥ 0

Dari gambar sifat-sifat perhitungan dari bentuk akar diatas kita bisa dengan mudah dalam menyelesaikan operasi hitungan aljabar bentuk akar tersebut dengan menggunakan rumus-rumus diatas.
Berikut contoh soal penjelasan dari konsep di atas :

Hitunglah operasi bentuk akar di bawah ini :
1. 4√2 + 7√2 + 2√2
2. 7√5 - 9√5 - 3√5
3. 6√3 + 9√3 - 2√3

Penyelesaian:
1. 4√2 + 7√2 + 2√2  = (4 + 7 +2)√2
                                  = 13√2
Jadi, penjumlahan dari 4√2 + 7√2 + 2√2  adalah 13√2

2. 7√5 - 9√5 - 3√5  = (7 – 9 – 3)√5
                                = -5√5
Jadi penjumlahan dari 7√5 - 9√5 - 3√5   adalah -5√5

3. 6√3+ 9√3- 2√3 = (6 + 9 -2) √3  = 13√3
Jadi hasil dari penjumlahannya adalah 133

Perkalian dan Pembagian Bentuk Akar

Sifat - sifat dari perkalian dan pembagian dalam bentuk akar bisa dijabarkan seperti berikut :

                                            a√b  x c√d  = ac √bd

                                            dengan a, b, c, d ∈R dan b ≥ 0, d ≥ 0

Untuk lebih jelasnya perhatikan contoh soal berikut :

a. √5 x √4

b. 7√5 x 9√3

Penyelesaian :

a. √5 x √4 = √(5 x 4) = √20

b. 7√5 x 9√3  = (7x9) x √5 x √3

                       = (7 x 9) x √(5 x 3)
                       = 63 x √15
                       = 63√15
Jadi hasil perkalian bentuk akar dari 7√5 x 9√3 adalah : 63√15.

Sifat pembagian bentuk akar diuraikan sebagai berikut :
                                                                                                a/√b  = √a/b
                                                                                                dengan a, b ∈R dan a ≥ 0, b ≥ 0
Contoh :
1. 8√10
     4√5
2. 2√4
    6√8

Penyelesaian :
Dalam penyelesaian operasi akar perkalian dan pembagian tidak jauh berbeda dengan mengoperasikan bentuk akar dengan penjumlahan dan juga pengurangan, sehingga :

Jadi hasil pembagian dari 8√10
                                             4√5  adalah : 2√2

Jadi hasil pembagian dari 2√4
                                            6√8 adalah : 0,3√0,5

Operasi Campuran Bentuk Akar

Prioritas yang paling utama dalam menyelesaikan soal - soal berbentuk bilangan campuran yaitu bilangan yang ada di dalam tanda kurung. Jika tidak ada tanda kurung maka :
1. Pangkat dan akar sama kuat
2. Perkalian dan pembagian sama kuat
3. Penjumlahan dan pengurangan sama kuat
4. Perkalian dan pembagian lebih kuat dari penjumlahan dan pengurangan

Contoh :
Selesaikanlah pecahan bentuk akar dibawah ini :
a. 2 / (√5 - √3)
b. 6 / (4√4 + √3)

Penyelesaian :
a. Untuk penyelesaian pecahan tersebut kita bisa menggunakan rumus a/(√a + √b), sehingga :
    2 / (√5 - √3) = 2 / (√5 - √3) x 2 / (√5 + √3) / √5 + √3)
                         = (2√5 + 2√3) / (5 - 3)
                         = (2√5 + 2√3) / 2
                         = √5 + √3
Jadi bisa diketahui bahwa hasil pecahan dari 2/(√5 - √3) adalah √5 + √3

b. 6 / (4√4 + √3) = 6 / (4√4 + √3 x 6 (4√4 - √3 / 6 (4√4 - √3
                            = (24√4 - 4√3) / (4-3)
                            = (24√4 - 4√3) /1

Itulah penjelasan dan contoh soal beserta pembahasan tentang Pengoperasian Aljabar Bentuk Akar, yang dijelaskan secara detail, sehingga bisa membantu dalam mengerjakan soal-soal matematika yang biasa kita temukan dalam pelajaran matematika. Semoga apa yang telah saya jelaskan di atas bisa membantu dalam penyelesaian soal-soal aljabar bentuk akar yang lainnya.

Baca Juga:

• Materi Matematika SD Kelas 4 Sifat - Sifat Operasi Hitung 
• Materi Matematika SMP Kelas 8 Bangun Ruang Sisi Lengkung 
• Rangkuman Materi Bangun Ruang Matematika SMP Kelas 8

Rangkuman Materi Urutan Pemusatan Data Mean, Median, Dan Modus Dilengkapi Pembahasan Contoh Soal Lengkap

Urutan Pemusatan Data Mean, Median, Dan Modus - Sebelum mempelajari contoh soal dan pembahasannya terlebih dahulu kita memahami arti dari Urutan pemusatan data, mean, median, dan modus. Berikut uraian penjelasannya.

Urutan Pemusatan Data

Urutan pemusatan data merupakan nilai maupun data yang mewakili dari sekelompok data yang biasa disebut dengan rata-rata. Nilai suatu rata-rata biasanya cenderung terletak di tengah-tengah suatu kelompok data yang di susun secara beruntun.

Mean

Mean atau rataan hitung merupakan jumlah keseluruhan data dari sekumpulan data yang ada  yang kemudian dibagi dengan banyaknya data yang ada. Mean dirumuskan seperti berikut :

Keterangan :

                     x = Jumlah data

                     n = Jumlah dari banyaknya data yang ada

Contoh soal 1 :
Diketahui 30 mahasiswa yang mengikuti ujian akhir semester dalam pelajaran matematika, memperoleh nilai masing-masing, Erik mendapat nilai 70, Sasa mendapat nilai 80, bagus mendapat nilai 75, Anindita mendapat nilai 70, Ilyas mendapat nilai 80, Tia mendapat nilai 70, Heru mendapat nilai 70, dan Diana mendapatkan nilai terendah yaitu 60.
Carilah nilai mean, dari sekumpulan data tersebut.

Pnyelesaian:

Nilai Mean : 

Kita gunakan rumus :

 

Dengan x merupakan jumlah data, dan n merupakan jumlah dari banyaknya data yang ada, sehingga :

Mean = 16,5 

Jadi mean dari data tersebut adalah 16,5

Median

Median merupakan nilai tengah dari sekumpulan data yang bisa diketahui dengan mengurutkan nilai -nilai terkecil hingga yang paling besar dari sekumpulan data tersebut. 

Contoh soal untuk mencari median, kita ambil sampel dari data di atas (contoh soal 1):

Dalam mencari median atau nilai tengah kita bisa memulainya dengan mengurutkan data dari yang terkecil hingga yang terbesar.
70, 75, 70, 80, 70, 70, 60 diurutkan menjadi 60 70, 70, 70, 70, 75, dan 80.
Setelah diurutkan maka ambillah nilai yang berada di tengah-tengah sekumpulan dari data tersebut.
Median = 70.

Jadi, median dari data di atas adalah 70.
Namun jika data yang ada berjumlah genap kita perlu mengambil dua nila yang di tengah yang kemudian dibagi 2. 

Misalkan menentukan median dari data : 60, 60 70, 70, 70, 75, 80, 80, 85

Maka mediannya adalah = 70 + 75 : 2 = 72,5

Modus

Modus merupakan nilai yang paling sering muncul pada sekumpulan data. 

Misalkan :

Diketahui data ulangan matematika kelas VIIIA adalah : 70, 70, 80, 75, 80, 75, 85, 85, 80

Penyelesaian :

Angka atau nilai 80 dari data tersebut muncul tiga (3) kali, maka modusnya adalah 80.

Apabila angka / nilai dari suatu data memiliki 2 modus (dua angka yang memiliki frekuensi yang sama), maka data tersebut disebut sebagai bimodus.

Contoh soal 2 :
Diketahui data ulangan dari sekolah dasar mekar sari, yang diikuti oleh 40 orang anak  yang  mendapatkan nilai ulangan masing-masing 60, 65, 60, 70, 75, 75, 80, 75, 80, 70.
Jadi hitunglah nilai dari mean, median, dan juga modus dari data tersebut !

Penyelesaian:
Mean :

Seperti halnya dengan soal yang pertama, soal yang ke dua ini kita juga bisa menggunakan rumus :

Mean = 17,75 

Setelah itu mencari median.pertama kita harus mengurutkan datanya terlebih dahulu
60, 65, 60, 70, 75, 75, 80, 75, 80, 70 menjadi: 60, 60, 65, 70, 70, 75, 75, 75, 80, 80.
Kemudian kita ambil data yang posisinya di tengah-tengah, karena data yang ada berjumlah genap, maka yang kita ambil adalah dua data yang paling tengah yaitu {70 dan 75} kemudian di bagi dua, sehingga : 

Median: 72,5 

Setelah selesai mencari median dan mean selanjutnya kita mencari modus, modus adalah nilai yang paling sering muncul dalam sekumpulan data, jadi bisa dengan mudah di tentukan nilai modus dari data diatas adalah 75. Karena 75 merupakan nilai yang paling sering muncul dari data tersebut.
Jadi bisa disimpulkan nilai mean adalah 17,75. Median 72.5 dan juga modusnya 75. Dari sekumpulan data : 60, 65, 60, 70, 75, 75, 80, 75, 80, 70. 

Sampai disini dulu penjelasan materi mengenai Urutan Pemusatan Data Mean, Median, Dan Modus Dilengkapi Pembahasan Contoh Soal. Semoga dari penjelasan dan contoh soal serta penyelesaian tentang pengurutan dari sekumpulan data diatas kalian bisa dengan mudah memahami, dan bisa membantu dalam menyelesaikan soal-soal matematika yang lainnya, semoga ini bisa memberikan manfaat untuk kita semua. Selamat Belajar.

Baca Juga :

Rangkuman Rumus Pada Integral Tigonometri
Materi Matematika Cara Mencari Simetri Putar Bangun Datar
Modus Ponens dan Tollens Logika Matematika